Spherical integral transforms of second-order gravitational tensor components onto third-order gravitational tensor components

Abstract

New spherical integral formulas between components of the second- and third-order gravitational tensors are formulated in this article. First, we review the nomenclature and basic properties of the second- and third-order gravitational tensors. Initial points of mathematical derivations, i.e., the second- and third-order differential operators defined in the spherical local North-oriented reference frame and the analytical solutions of the gradiometric boundary-value problem, are also summarized. Secondly, we apply the third-order differential operators to the analytical solutions of the gradiometric boundary-value problem which gives 30 new integral formulas transforming (1) vertical-vertical, (2) vertical-horizontal and (3) horizontal-horizontal second-order gravitational tensor components onto their third-order counterparts. Using spherical polar coordinates related sub-integral kernels can efficiently be decomposed into azimuthal and isotropic parts. Both spectral and closed forms of the isotropic kernels are provided and their limits are investigated. Thirdly, numerical experiments are performed to test the consistency of the new integral transforms and to investigate properties of the sub-integral kernels. The new mathematical apparatus is valid for any harmonic potential field and may be exploited, e.g., when gravitational/magnetic second- and third-order tensor components become available in the future. The new integral formulas also extend the well-known Meissl diagram and enrich the theoretical apparatus of geodesy.

Appendices

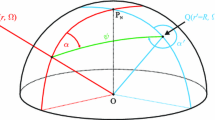
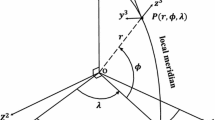
Appendix A: Formulas for $u = \cos \psi$, direct azimuth $\alpha$ and backward azimuth $\alpha '$

In this appendix, we provide equations for numerical calculation of the parameter $u = \cos \psi$, direct azimuth $\alpha$ and backward azimuth $\alpha '$. Given the spherical coordinates of the evaluation and integration points, these parameters are defined as follows:

$$\begin{aligned} u = \cos \psi = \sin \varphi \sin \varphi ' + \cos \varphi \cos \varphi ' \cos (\lambda ' - \lambda ), \end{aligned}$$

(34a)

$$\begin{aligned} \cos \alpha= & {} \frac{1}{\sqrt{1 - u^2}} \big [ \sin \varphi ' \cos \varphi \nonumber \\&- \cos \varphi ' \sin \varphi \cos (\lambda ' - \lambda )\ \big ], \end{aligned}$$

(34b)

$$\begin{aligned} \sin \alpha = \frac{1}{\sqrt{1 - u^2}}\ \cos \varphi ' \sin (\lambda ' - \lambda ), \end{aligned}$$

(34c)

$$\begin{aligned} \cos \alpha '= & {} \frac{1}{\sqrt{1 - u^2}} \big [ \sin \varphi \cos \varphi ' \nonumber \\&- \cos \varphi \sin \varphi ' \cos (\lambda ' - \lambda )\ \big ], \end{aligned}$$

(34d)

$$\begin{aligned} \sin \alpha ' = \frac{- 1}{\sqrt{1 - u^2}}\ \cos \varphi \sin (\lambda ' - \lambda ). \end{aligned}$$

(34e)

Equations (34a)–(34e) can be derived by using cosine, sine and sine-cosine rules of spherical trigonometry, see, e.g., Chauvenet (1875, pp. 151–154).

Cosines and sines of multiples of $\alpha$ and $\alpha '$ also appear in Sect. 3. They read

$$\begin{aligned} \cos 2 \alpha = 2 \cos ^2 \alpha - 1, \end{aligned}$$

(35a)

$$\begin{aligned} \sin 2 \alpha = 2 \cos \alpha \sin \alpha , \end{aligned}$$

(35b)

$$\begin{aligned} \cos 3 \alpha = \cos \alpha \ (\cos ^2 \alpha - 3 \sin ^2 \alpha ), \end{aligned}$$

(35c)

$$\begin{aligned} \sin 3 \alpha = - \sin \alpha \ (\sin ^2 \alpha - 3 \cos ^2 \alpha ), \end{aligned}$$

(35d)

$$\begin{aligned} \cos 2 \alpha ' = 2 \cos ^2 \alpha ' - 1, \end{aligned}$$

(35e)

$$\begin{aligned} \sin 2 \alpha ' = 2 \cos \alpha ' \sin \alpha '. \end{aligned}$$

(35f)

Equations (35a)–(35f) can be obtained from the multiple-angle formulas for trigonometric functions, see, e.g., Abramowitz and Stegun (1972), p. 72.

Appendix B: Action of the third-order differential operators on multiplication of two functions

In this appendix, the general form resulting from the application of the third-order differential operators on multiplication of two functions is provided. This is exploited in Sects. 3.2 and 3.3 to derive integral transforms of the VH and HH gravitational tensor components onto the third-order gravitational tensor components.

We suppose two functions, i.e., $f = f(\Omega ,\Omega ')$ and $h = h (r,R,\Omega ,\Omega ')$. The function f depends only on the geocentric angular coordinates, while h also depends on the geocentric radii of the evaluation and integration points. We now apply the recursive formulas between the second- and third-order differential operators of Eq. (12) to the multiplication of f and h that gives:

$$\begin{aligned} \mathcal{{D}}^{xxx}(f\ h)&= f\ \mathcal{{D}}^{xxx} h + h\ \mathcal{{D}}^{xxx} f + \frac{1}{r} \frac{\partial f}{\partial \varphi }\ \mathcal{{D}}^{xx} h\nonumber \\&\quad + \frac{1}{r} \frac{\partial h}{\partial \varphi }\ \mathcal{{D}}^{xx} f + \frac{2}{r^2} \frac{\partial h}{\partial r} \frac{\partial f}{\partial \varphi }\nonumber \\&\quad + \frac{2}{r^3} \frac{\partial }{\partial \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \varphi } \right) , \end{aligned}$$

(36a)

$$\begin{aligned} \mathcal{{D}}^{xxy}(f\ h)&= f\ \mathcal{{D}}^{xxy} h + h\ \mathcal{{D}}^{xxy} f + \frac{1}{r} \frac{\partial f}{\partial \varphi }\ \mathcal{{D}}^{xy} h\nonumber \\&\quad + \frac{1}{r} \frac{\partial h}{\partial \varphi }\ \mathcal{{D}}^{xy} f - \frac{1}{r^2 \cos \varphi } \frac{\partial h}{\partial r} \frac{\partial f}{\partial \lambda }\nonumber \\&\quad - \frac{1}{r} \frac{\partial }{\partial \varphi } \left[ \frac{1}{r^2 \cos \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \lambda } + \frac{\partial h}{\partial \varphi } \frac{\partial f}{\partial \lambda } \right) \right] , \end{aligned}$$

(36b)

$$\begin{aligned} \mathcal{{D}}^{xxz}(f\ h)&= f\ \mathcal{{D}}^{xxz} h + h\ \mathcal{{D}}^{xxz} f + \frac{\partial h}{\partial r}\ \mathcal{{D}}^{xx} f\nonumber \\&\quad + \frac{\partial }{\partial r} \left( \frac{2}{r^2} \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \varphi } \right) , \end{aligned}$$

(36c)

$$\begin{aligned} \mathcal{{D}}^{xyy}(f\ h)&= f\ \mathcal{{D}}^{xyy} h + h\ \mathcal{{D}}^{xyy} f\nonumber \\&\quad + \frac{1}{r} \frac{\partial f}{\partial \varphi }\ \mathcal{{D}}^{yy} h + \frac{1}{r} \frac{\partial h}{\partial \varphi }\ \mathcal{{D}}^{yy} f\nonumber \\&\quad + \frac{1}{r} \frac{\partial }{\partial \varphi } \left( \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial f}{\partial \lambda } \frac{\partial h}{\partial \lambda } \right) , \end{aligned}$$

(36d)

$$\begin{aligned} \mathcal{{D}}^{xyz}(f\ h)&= f\ \mathcal{{D}}^{xyz}\ h + h \mathcal{{D}}^{xyz} \ f + \frac{\partial h}{\partial r} \mathcal{{D}}^{xy} \ f\nonumber \\&\quad - \frac{\partial }{\partial r} \left[ \frac{1}{r^2 \cos \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \lambda } + \frac{\partial h}{\partial \varphi } \frac{\partial f}{\partial \lambda } \right) \right] , \end{aligned}$$

(36e)

$$\begin{aligned} \mathcal{{D}}^{xzz}(f\ h)&= f\ \mathcal{{D}}^{xzz}\ h + h\ \mathcal{{D}}^{xzz}\ f \nonumber \\&\quad + \frac{\partial h}{\partial r}\ \mathcal{{D}}^{xz}\ f + \frac{\partial }{\partial r} \left( \frac{1}{r} \frac{\partial h}{\partial r} \frac{\partial f}{\partial \varphi } \right) , \end{aligned}$$

(36f)

$$\begin{aligned} \mathcal{{D}}^{yyy}(f\ h)&= f\ \mathcal{{D}}^{yyy}\ h + h\ \mathcal{{D}}^{yyy}\ f - \frac{1}{r \cos \varphi } \frac{\partial f}{\partial \lambda }\ \mathcal{{D}}^{yy}\ h \nonumber \\&\quad - \frac{1}{r \cos \varphi } \frac{\partial h}{\partial \lambda }\ \mathcal{{D}}^{yy}\ f- \frac{2}{r^2 \cos \varphi } \frac{\partial h}{\partial r} \frac{\partial f}{\partial \lambda } \nonumber \\&\quad + \frac{2 \tan \varphi }{r^3 \cos \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \lambda } + \frac{\partial h}{\partial \varphi } \frac{\partial f}{\partial \lambda } \right) \nonumber \\&\quad - \frac{1}{r \cos \varphi } \frac{\partial }{\partial \lambda } \left( \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial f}{\partial \lambda } \frac{\partial h}{\partial \lambda } \right) , \end{aligned}$$

(36g)

$$\begin{aligned} \mathcal{{D}}^{yyz}(f\ h)&= f\ \mathcal{{D}}^{yyz}\ h + h\ \mathcal{{D}}^{yyz}\ f + \frac{\partial h}{\partial r}\ \mathcal{{D}}^{yy}\ f \nonumber \\&\quad + \frac{\partial }{\partial r} \left( \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial f}{\partial \lambda } \frac{\partial h}{\partial \lambda } \right) , \end{aligned}$$

(36h)

$$\begin{aligned} \mathcal{{D}}^{yzz}(f\ h)&= f\ \mathcal{{D}}^{yzz}\ h + h\ \mathcal{{D}}^{yzz}\ f + \frac{\partial h}{\partial r}\ \mathcal{{D}}^{yz}\ f \nonumber \\&\quad - \frac{\partial }{\partial r} \left( \frac{1}{r \cos \varphi } \frac{\partial h}{\partial r} \frac{\partial f}{\partial \lambda } \right) , \end{aligned}$$

(36i)

$$\begin{aligned} \mathcal{{D}}^{zzz}(f\ h) = f\ \mathcal{{D}}^{zzz}\ h. \end{aligned}$$

(36j)

Appendix C: Derivatives of the backward azimuth $\alpha '$

In Eqs. (36a)–(36i), the first-order derivatives with respect to the spherical geocentric angular coordinates $\varphi$ and $\lambda$ as well as the second- and third-order differential operators are applied to the function f. In this appendix, we provide formulas for the action of such differential operators assuming $f = \cos \alpha '$, $\sin \alpha '$, $\cos 2 \alpha '$ and $\sin 2\alpha '$. These are expressed in terms of the parameters $t, u, \alpha$ and $\alpha '$, and exploited for the mathematical derivations in Sect. 3.

The first-order derivatives of $\cos \alpha '$ read as follows, see, e.g., Winch and Roberts (1995):

$$\begin{aligned} \frac{\partial \cos \alpha '}{\partial \varphi } = \frac{- 1}{\sqrt{1 - u^2}}\ \sin \alpha ' \sin \alpha , \end{aligned}$$

(37a)

$$\begin{aligned} \frac{\partial \cos \alpha '}{\partial \lambda } = \frac{\cos \varphi }{\sqrt{1 - u^2}}\ \sin \alpha ' \cos \alpha . \end{aligned}$$

(37b)

We can easily obtain:

• derivatives of $\sin \alpha '$ by changing $\sin \alpha ' \rightarrow - \cos \alpha '$,

• derivatives of $\cos 2\alpha '$ by changing $\sin \alpha ' \rightarrow 2\sin 2\alpha '$,

• derivatives of $\sin 2\alpha '$ by changing $\sin \alpha ' \rightarrow - 2\cos 2\alpha '$,

in Eqs. (37a)–(37b).

Formulas for the action of the second-order operators $\mathcal{{D}}^{xx}$, $\mathcal{{D}}^{xy}$, $\mathcal{{D}}^{xz}$, $\mathcal{{D}}^{yy}$ and $\mathcal{{D}}^{yz}$ to $\cos \alpha '$ are of the form (Šprlák et al. 2014):

$$\begin{aligned} \mathcal{{D}}^{xx} \cos \alpha '&= \frac{- t^2}{2 R^2 (1 - u^2)}\nonumber \\&\quad \times \big [ \cos \alpha ' (1 - \cos 2 \alpha ) + 2 u \sin \alpha ' \sin 2 \alpha \big ], \end{aligned}$$

(38a)

$$\begin{aligned} \mathcal{{D}}^{xy} \cos \alpha '&= \frac{- t^2}{2 R^2 (1 - u^2)}\nonumber \\&\quad \times (\cos \alpha ' \sin 2 \alpha + 2 u \sin \alpha ' \cos 2 \alpha ), \end{aligned}$$

(38b)

$$\begin{aligned} \mathcal{{D}}^{xz} \cos \alpha ' = \frac{t^2}{R^2 \sqrt{1 - u^2}}\ \sin \alpha ' \sin \alpha , \end{aligned}$$

(38c)

$$\begin{aligned} \mathcal{{D}}^{yy} \cos \alpha '= & {} \frac{- t^2}{2 R^2 (1 - u^2)} \big [ \cos \alpha ' (1 + \cos 2 \alpha ) \nonumber \\&- 2 u \sin \alpha ' \sin 2 \alpha \big ], \end{aligned}$$

(38d)

$$\begin{aligned} \mathcal{{D}}^{yz} \cos \alpha ' = \frac{t^2}{R^2 \sqrt{1 - u^2}}\ \sin \alpha ' \cos \alpha . \end{aligned}$$

(38e)

One can also obtain the action of the second-order differential operators to:

• $\sin \alpha '$ by changing $\sin \alpha ' \rightarrow - \cos \alpha '$ and $\cos \alpha ' \rightarrow \sin \alpha '$,

• $\cos 2\alpha '$ by changing $\sin \alpha ' \rightarrow 2\sin 2\alpha '$ and $\cos \alpha ' \rightarrow 4 \cos 2\alpha '$,

• $\sin 2\alpha '$ by changing $\sin \alpha ' \rightarrow - 2\cos 2\alpha '$ and $\cos \alpha ' \rightarrow 4 \sin 2\alpha '$,

in Eqs. (38a)–(38e).

By applying the third-order differential operators $\mathcal{{D}}^{xxx}$, $\mathcal{{D}}^{xxy}$, $\mathcal{{D}}^{xxz}$, $\mathcal{{D}}^{xyy}$, $\mathcal{{D}}^{xyz}$, $\mathcal{{D}}^{xzz}$, $\mathcal{{D}}^{yyy}$, $\mathcal{{D}}^{yyz}$ and $\mathcal{{D}}^{yzz}$ to $\cos \alpha '$ we get:

$$\begin{aligned} \mathcal{{D}}^{xxx} \cos \alpha '&= \frac{3 t^3}{4 R^3 (1 - u^2)^{3/2}}\big [ \sin \alpha ' (3 \sin \alpha - \sin 3 \alpha ) \nonumber \\&\quad - 2 u \cos \alpha ' (\cos \alpha - \cos 3 \alpha )\nonumber \\&\quad - 2 u^2 \sin \alpha ' (\sin \alpha + \sin 3 \alpha )\big ], \end{aligned}$$

(39a)

$$\begin{aligned} \mathcal{{D}}^{xxy} \cos \alpha '&= \frac{t^3}{4 R^3 (1 - u^2)^{3/2}}\big [ 3 \sin \alpha ' (\cos \alpha - \cos 3 \alpha ) \nonumber \\&\quad + 2 u \cos \alpha ' (\sin \alpha - 3 \sin 3 \alpha )\nonumber \\&\quad - 2 u^2 \sin \alpha ' (\cos \alpha + 3 \cos 3 \alpha )\big ], \end{aligned}$$

(39b)

$$\begin{aligned} \mathcal{{D}}^{xxz} \cos \alpha '&= \frac{t^3}{R^3 (1 - u^2)}\big [ \cos \alpha ' (1 - \cos 2 \alpha ) \nonumber \\&\quad + 2 u \sin \alpha ' \sin 2 \alpha \big ], \end{aligned}$$

(39c)

$$\begin{aligned} \mathcal{{D}}^{xyy} \cos \alpha '&= \frac{t^3}{4 R^3 (1 - u^2)^{3/2}}\ \big [ 3 \sin \alpha ' (\sin \alpha + \sin 3 \alpha )\nonumber \\&\quad - 2 u \cos \alpha ' (\cos \alpha + 3 \cos 3 \alpha )\nonumber \\&\quad - 2 u^2 \sin \alpha ' (\sin \alpha - 3 \sin 3 \alpha )\big ], \end{aligned}$$

(39d)

$$\begin{aligned} \mathcal{{D}}^{xyz} \cos \alpha '= & {} \frac{t^3}{R^3 (1 - u^2)}\ (\cos \alpha ' \sin 2\alpha \nonumber \\&+ 2 u \sin \alpha ' \cos 2\alpha ), \end{aligned}$$

(39e)

$$\begin{aligned} \mathcal{{D}}^{xzz} \cos \alpha ' = \frac{-2 t^3}{R^3 \sqrt{1 - u^2}}\ \sin \alpha ' \sin \alpha , \end{aligned}$$

(39f)

$$\begin{aligned} \mathcal{{D}}^{yyy} \cos \alpha '&= \frac{3 t^3}{4 R^3 (1 - u^2)^{3/2}}\ \big [ \sin \alpha ' (3 \cos \alpha + \cos 3 \alpha )\nonumber \\&\quad + 2 u \cos \alpha ' (\sin \alpha + \sin 3 \alpha )\nonumber \\&\quad - 2 u^2 \sin \alpha ' (\cos \alpha - \cos 3 \alpha )\big ], \end{aligned}$$

(39g)

$$\begin{aligned} \mathcal{{D}}^{yyz} \cos \alpha '= & {} \frac{t^3}{R^3 (1 - u^2)} \big [ \cos \alpha ' (1 + \cos 2 \alpha )\nonumber \\&- 2 u \sin \alpha ' \sin 2\alpha \ \big ], \end{aligned}$$

(39h)

$$\begin{aligned} \mathcal{{D}}^{yzz} \cos \alpha ' = \frac{-2 t^3}{R^3 \sqrt{1 - u^2}}\ \sin \alpha ' \cos \alpha . \end{aligned}$$

(39i)

We arrive at the formulas for the application of the third-order differential operators for:

• $\sin \alpha '$ by changing $\sin \alpha ' \rightarrow - \cos \alpha '$ and $\cos \alpha ' \rightarrow \sin \alpha '$.

• $\cos 2\alpha '$ by changing $\cos \alpha ' \rightarrow 4 \cos 2\alpha '$; in addition, we change $\sin \alpha ' \rightarrow 2\sin 2\alpha '$ for the operators $\mathcal{{D}}^{xxz}$, $\mathcal{{D}}^{xyz}$, $\mathcal{{D}}^{xzz}$, $\mathcal{{D}}^{yyz}$ and also when $\sin \alpha '$ is multiplied by $u^2$, i.e., in the third terms inside the square brackets for the operators $\mathcal{{D}}^{xxx}$, $\mathcal{{D}}^{xxy}$, $\mathcal{{D}}^{xyy}$ and $\mathcal{{D}}^{yyy}$; for the purely horizontal operators, another change $\sin \alpha ' \rightarrow 4\sin 2\alpha '$ is applied in the first terms inside the square brackets,

• $\sin 2\alpha '$ by changing $\cos \alpha ' \rightarrow 4 \sin 2\alpha '$; moreover, the substitution $\sin \alpha ' \rightarrow - 2\cos 2\alpha '$ is applied for the operators $\mathcal{{D}}^{xxz}$, $\mathcal{{D}}^{xyz}$, $\mathcal{{D}}^{xzz}$, $\mathcal{{D}}^{yyz}$ and also when $\sin \alpha '$ is multiplied by $u^2$ in the third terms inside the square brackets for the operators $\mathcal{{D}}^{xxx}$, $\mathcal{{D}}^{xxy}$, $\mathcal{{D}}^{xyy}$ and $\mathcal{{D}}^{yyy}$; for the purely horizontal differential operators, we also change $\sin \alpha ' \rightarrow -4\cos 2\alpha '$ in the first terms inside the square brackets,

in Eqs. (39a)–(39i).

Appendix D: Auxiliary terms from the action of the third-order differential operators on multiplication of two functions

In this appendix, formulas for the auxiliary terms in Eqs. (36a)–(36i), i.e., all terms except for the action of the second and third-order differential operators, are provided. Similar to “Appendix C”, the auxiliary terms are given for $f = \cos \alpha '$, $\sin \alpha '$, $\cos 2 \alpha '$ and $\sin 2\alpha '$ in terms of the parameters t, u, $\alpha$ and $\alpha '$. However, we still assume the general function $h = h (r,R,\Omega ,\Omega ')$ specified in Sect. 3.

The auxiliary terms of Eqs. (36a)–(36i) for $f = \cos \alpha '$ read:

$$\begin{aligned}&\frac{2}{r^2} \frac{\partial h}{\partial r} \frac{\partial f}{\partial \varphi } + \frac{2}{r^3} \frac{\partial }{\partial \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \varphi } \right) \nonumber \\&\quad = \frac{t^3}{R^3}\Bigg \{\sin \alpha ' \Bigg [\sin \alpha \Bigg (\frac{2t}{\sqrt{1-u^2}} \frac{\partial h}{\partial t} + \frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u}\nonumber \\&\qquad - \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2}\Bigg ) - \sin 3 \alpha \left( \frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u}\right. \nonumber \\&\qquad \left. + \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2}\right) \Bigg ]- \frac{\cos \alpha ' \left( \cos \alpha - \cos 3 \alpha \right) }{2 \sqrt{1-u^2}} \frac{\partial h}{\partial u} \Bigg \}, \end{aligned}$$

(40a)

$$\begin{aligned}&- \frac{1}{r^2 \cos \varphi } \frac{\partial h}{\partial r} \frac{\partial f}{\partial \lambda } - \frac{1}{r} \frac{\partial }{\partial \varphi } \left[ \frac{1}{r^2 \cos \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \lambda } + \frac{\partial h}{\partial \varphi } \frac{\partial f}{\partial \lambda } \right) \right] \nonumber \\&\quad = \frac{t^3}{R^3} \Bigg \{\sin \alpha ' \Bigg [\cos \alpha \left( \frac{t}{\sqrt{1-u^2}} \frac{\partial h}{\partial t} \right. \nonumber \\&\quad \quad \left. +\frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u} - \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2}\right) \nonumber \\&\qquad - \cos 3 \alpha \left( \frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u} + \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2}\right) \Bigg ]\nonumber \\&\qquad + \frac{\cos \alpha ' \left( \sin \alpha - \sin 3 \alpha \right) }{2 \sqrt{1-u^2}} \frac{\partial h}{\partial u} \Bigg \}, \end{aligned}$$

(40b)

$$\begin{aligned} \frac{\partial }{\partial r} \left( \frac{2}{r^2} \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \varphi } \right) = \frac{t^3}{R^3} \sin \alpha ' \sin 2 \alpha \left( 2 \frac{\partial h}{\partial u} + t \frac{\partial ^2 h}{\partial t \partial u}\right) ,\nonumber \\ \end{aligned}$$

(40c)

$$\begin{aligned}&\frac{1}{r} \frac{\partial }{\partial \varphi } \left( \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial f}{\partial \lambda } \frac{\partial h}{\partial \lambda } \right) \nonumber \\&\quad = \frac{t^3}{R^3}\Bigg \{\sin \alpha ' \Bigg [\sin \alpha \left( \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2} - \frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u}\right) \nonumber \\&\quad + \sin 3 \alpha \left( \frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u} + \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2}\right) \Bigg ]\nonumber \\&\quad + \frac{\cos \alpha ' \left( \cos \alpha - \cos 3 \alpha \right) }{2 \sqrt{1-u^2}} \frac{\partial h}{\partial u} \Bigg \}, \end{aligned}$$

(40d)

$$\begin{aligned}&- \frac{\partial }{\partial r} \left[ \frac{1}{r^{2} \cos \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \lambda } + \frac{\partial h}{\partial \varphi } \frac{\partial f}{\partial \lambda } \right) \right] \nonumber \\&\quad = \frac{t^3}{R^3} \sin \alpha ' \cos 2 \alpha \left( 2 \frac{\partial h}{\partial u} + t \frac{\partial ^2 h}{\partial t \partial u}\right) , \end{aligned}$$

(40e)

$$\begin{aligned}&\frac{\partial }{\partial r} \left( \frac{1}{r} \frac{\partial h}{\partial r} \frac{\partial f}{\partial \varphi } \right) \nonumber \\&\quad = - \frac{t^4}{R^3 \sqrt{1-u^2}} \sin \alpha ' \sin \alpha \left( 3 \frac{\partial h}{\partial t} + t \frac{\partial ^2 h}{\partial t^2}\right) , \end{aligned}$$

(40f)

$$\begin{aligned}&- \frac{2}{r^2 \cos \varphi } \frac{\partial h}{\partial r} \frac{\partial f}{\partial \lambda } + \frac{2 \tan \varphi }{r^3 \cos \varphi } \left( \frac{\partial f}{\partial \varphi } \frac{\partial h}{\partial \lambda } + \frac{\partial h}{\partial \varphi } \frac{\partial f}{\partial \lambda } \right) \nonumber \\&\qquad - \frac{1}{r \cos \varphi } \frac{\partial }{\partial \lambda } \left( \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial f}{\partial \lambda } \frac{\partial h}{\partial \lambda } \right) \nonumber \\&\quad = \frac{t^3}{R^3} \Bigg \{\sin \alpha ' \Bigg [\cos \alpha \left( \frac{2t}{\sqrt{1-u^2}} \frac{\partial h}{\partial t}\right. \nonumber \\&\quad \left. + \frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u} - \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2}\right) \nonumber \\&\qquad + \cos 3 \alpha \left( \frac{u}{\sqrt{1-u^2}} \frac{\partial h}{\partial u} + \frac{\sqrt{1-u^2}}{2} \frac{\partial ^2 h}{\partial u^2}\right) \Bigg ] \nonumber \\&\quad + \frac{\cos \alpha ' \left( \sin \alpha + \sin 3 \alpha \right) }{2 \sqrt{1-u^2}} \frac{\partial h}{\partial u} \Bigg \}, \end{aligned}$$

(40g)

$$\begin{aligned}&\frac{\partial }{\partial r} \left( \frac{2}{r^2 \cos ^2 \varphi } \frac{\partial f}{\partial \lambda } \frac{\partial h}{\partial \lambda } \right) \nonumber \\&\quad = - \frac{t^3}{R^3} \sin \alpha ' \sin 2\alpha \left( 2 \frac{\partial h}{\partial u} + t \frac{\partial ^2 h}{\partial t \partial u}\right) , \end{aligned}$$

(40h)

$$\begin{aligned}&- \frac{\partial }{\partial r} \left( \frac{1}{r \cos \varphi } \frac{\partial h}{\partial r} \frac{\partial f}{\partial \lambda } \right) \nonumber \\&\quad = - \frac{t^4}{R^3 \sqrt{1-u^2}} \sin \alpha ' \cos \alpha \left( 3 \frac{\partial h}{\partial t} + t \frac{\partial ^2 h}{\partial t^2}\right) . \end{aligned}$$

(40i)

We can also obtain the auxiliary terms for:

• $f = \sin \alpha '$ by changing $\sin \alpha ' \rightarrow - \cos \alpha '$ and $\cos \alpha ' \rightarrow \sin \alpha '$,

• $f = \cos 2\alpha '$ by changing $\sin \alpha ' \rightarrow 2\sin 2\alpha '$ and $\cos \alpha ' \rightarrow 4 \cos 2\alpha '$,

• $f = \sin 2\alpha '$ by changing $\sin \alpha ' \rightarrow - 2\cos 2\alpha '$ and $\cos \alpha ' \rightarrow 4 \sin 2\alpha '$,

in Eqs. (40a)–(40i).