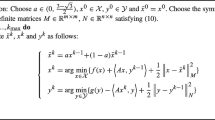Abstract
Markov Chain Monte Carlo (MCMC) algorithms play an important role in statistical inference problems dealing with intractable probability distributions. Recently, many MCMC algorithms such as Hamiltonian Monte Carlo (HMC) and Riemannian Manifold HMC have been proposed to provide distant proposals with high acceptance rate. These algorithms, however, tend to be computationally intensive which could limit their usefulness, especially for big data problems due to repetitive evaluations of functions and statistical quantities that depend on the data. This issue occurs in many statistic computing problems. In this paper, we propose a novel strategy that exploits smoothness (regularity) in parameter space to improve computational efficiency of MCMC algorithms. When evaluation of functions or statistical quantities are needed at a point in parameter space, interpolation from precomputed values or previous computed values is used. More specifically, we focus on HMC algorithms that use geometric information for faster exploration of probability distributions. Our proposed method is based on precomputing the required geometric information on a set of grids before running sampling algorithm and approximating the geometric information for the current location of the sampler using the precomputed information at nearby grids at each iteration of HMC. Sparse grid interpolation method is used for high dimensional problems. Tests on computational examples are shown to illustrate the advantages of our method.














Similar content being viewed by others
References
Ahmadian Y, Pillow JW, Paninski L (2011) Efficient Markov chain Monte Carlo methods for decoding neural spike trains. Neural Comput 23:46–96
Ahn S, Chen Y, Welling M (2013) Distributed and adaptive darting monte carlo through regenerations. In: International conference on artificial intelligence and statistics
Ahn S, Shahbaba B, Welling M (2014) Distributed stochastic gradient MCMC. In: International conference on machine learning
Alder BJ, Wainwright TE (1959) Studies in molecular dynamics. I. General method. J Chem Phys 31(1959):459–466
Barthelmann V, Novak E, Ritter K (2000) High dimensional polynomial interpolation on sparse grids. Adv Comput Math 12:273–288
Beskos A, Pinski FJ, Sanz-Serna JM, Stuart AM (2011) Hybrid monte-carlo on hilbert spaces. Stoch Process Appl 121:2201–2230
Bungartz HJ (1998) Finite elements of higher order on sparse grids. Sharker Verlag
Bungartz HJ, Griebel M (2004) Sparse grids. Acta Numer. 13:147–169
Calderhead B, Sustik M (2012) Sparse approximate manifolds for differential geometric mcmc. In: Bartlett P, Pereira FCN, Burges CJC, Bottou L, Weinberger KQ (eds) Advances in neural information processing systems 25, pp 2888–2896
Chen T, Fox EB, Guestrin C (2014) Stochastic gradient hamiltonian monte carlo. Preprint
Conard PR, Marzouk YM, Pillai NS, Smith A (2014) Asymptotically exact mcmc algorithms via local approximations of computationally intensive models. pp 1–38, arXiv:1402.1694v1
Dashti M, Stuart AM (2011) Uncertainty quantification and weak approximation of an elliptic inverse problem. SIAM J. Numer. Anal. 6:2524–2542
Duane S, Kennedy AD, Pendleton BJ, Roweth D (1987) Hybrid Monte Carlo. Phys Lett B 195:216–222
Geyer CJ (1992) Practical Markov Chain Monte Carlo. Stat Sci 7:473–483
Girolami M, Calderhead B (2011) Riemann manifold Langevin and Hamiltonian Monte Carlo methods. J R Stat Soc Ser B 73:123–214
Hoffman M, Gelman A (2011) The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. arXiv:1111.4246
Hoffman, M, Blei DM, Bach FR (2010) Online learning for latent dirichlet allocation. In: Lafferty JD, Williams CKI, Shawe-Taylor J, Zemel RS, Culotta A (eds) NIPS. Curran Associates, Inc., NY, pp 856–864
Klimke A, Wohlmuth B (2005) Algorithm 847: spinterp: piecewise multilinear hierarchical sparse grid interpolation in matlab 31:561–579
Lan S, Zhou B, Shahbaba B (2014) Spherical Hamiltonian Monte Carlo for constrained target distributions. In: 31th International conference on machine learning (to appear)
Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) Equation of state calculations by fast computing machines. J Chem Phys 21:1087–1092
Neal RM (1998) Regression and classification using Gaussian process priors. Bayesian Stat 6:471–501
Neal RM (2011) MCMC using Hamiltonian dynamics. In: Brooks S, Gelman A, Jones G, Meng XL (eds) Handbook of Markov Chain Monte Carlo, Chapman and Hall/CRC, pp 113–162
Rasmussen CE (1996) Evaluation of Gaussian processes and other methods for non-linear regression. Ph.D. thesis, Department of Computer Science, University of Toronto
Rasmussen CE (2003) Gaussian processes to speed up hybrid monte carlo for expensive bayesian integrals. In: Bayesian statistics, pp 651–659
Shahbaba B, Lan S, Johnson WO, Neal RM (2014) Split Hamiltonian Monte Carlo. Stat Comput 24:339–349
Wasilkowski GW, Wozoniakowski H (1995) Explicit cost bounds of algorithms for multivariate tensor product problems. J Complex 11:1–56
Welling M, Teh YW (2011) Bayesian learning via stochastic gradient langevin dynamics. In: Proceedings of the 28th international conference on machine learning (ICML), pp 681–688
Acknowledgments
We thank Wataru Sakamoto for his careful reading of the manuscript and useful feedbacks. We also thank the anonymous referees for suggestions that improved the exposition of this work. In addition, we appreciate the discussions with S. Lan and T. Chen. C. Zhang and H. Zhao were partially supported by NSF Grant DMS-1418422. B. Shahbaba and H. Zhao are partially supported by NSD Grant DMS-1622490.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Convergence to the correct distribution
In order to prove that the equilibrium distribution remains the same, it suffices to show that the detailed balance condition still holds. Note that the alternative Hamiltonian \(\tilde{H}(q,p)\) defines a surrogate-induced Hamiltonian flow, parameterized by the trajectory length t, which is a map \(\tilde{\phi }_t:\;(q,p)\rightarrow (q^*,p^{*})\). Here, \((q^*,p^*)\) is the end-point of the trajectory governed by the following equations
Denote \(\theta =(q,p),\;\theta '=(q^*,p^*)=\tilde{\phi }_t(\theta )\). In the Metropolis-Hasting step, we use the original Hamiltonian to compute the acceptance probability
therefore,
since \( \left| \frac{d\theta }{d\theta '}\right| = 1\) due to the volume conservation property of the surrogate induced Hamiltonian flow \(\tilde{\phi }_t\). Now that we showed the detailed balance condition is satisfied, along with the reversibility of the surrogate induced Hamiltonian flow, the modified Markov chain will converge to the correct target distribution.
Appendix 2: More on sparse grid
1.1 Construction of sparse grid and basis functions
The Clenshaw–Curtis type sparse grid \(H^{CC}\) introduced in Sect. 3.4.2 is constructed from the following formulas. Here, the \(x_j^i\) are defined as
In order to obtain nested sets of points, the number of nodes is given by
Piecewise linear basis functions a can be used for the univariate interpolation formulas \(U^i(f)\).
for \(i>1\) and \(j =1,\ldots ,m_i\).
1.2 Derivation of the hierarchical form
With the selection of nested sets of points, we can easily transform the univariate nodal basis into the hierarchical one. By definition, we have
since \(f(x_j^i) - U^{i-1}(f)(x_j^i) = 0,\; \forall \; x_j^i \in X^{i-1}\),
From (6.1) we note that for all \(\Delta ^i(f)\), only the basis functions belonging to the grid points that have not yet occurred in a previous set \(X^{i-k},\;1\le k \le i-1\) are involved. Figure 15 gives a comparison of the nodal and the hierarchical basis functions and Fig. 16 shows the construction of the interpolation formula using nodal basis functions and function values versus using hierarchical basis functions and hierarchical surpluses for a univariate function f. Both figures are reproductions based on Klimke and Wohlmuth (2005).
Applying the tensor product formula (3.7) with \(\Delta ^i\) given in (6.1), the hierarchical update in the Smolyak algorithm (3.8) now can be rewritten as
Rights and permissions
About this article
Cite this article
Zhang, C., Shahbaba, B. & Zhao, H. Precomputing strategy for Hamiltonian Monte Carlo method based on regularity in parameter space. Comput Stat 32, 253–279 (2017). https://doi.org/10.1007/s00180-016-0683-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00180-016-0683-1