Abstract
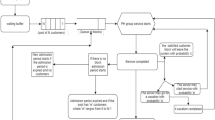
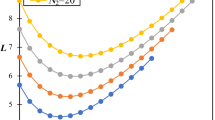
We study the effect of arrival model uncertainties on the optimal routing in a system of parallel queues. For exponential service time distributions and Bernoulli routing, the optimal mean system delay generally depends on the interarrival time distribution. Any error in modeling the arriving process will cause a model-based optimal routing algorithm to produce a mean system delay higher than the true optimum. In this paper, we present an asymptotic analysis of the behavior of this error under heavy traffic conditions for a general renewal arrival process. An asymptotic analysis of the error in optimal mean delay due to uncertainties in the service time distribution for Poisson arrivals was reported in Ref. 6, where it was shown that, when the first moment of the service time distribution is known, this error in performance vanishes asymptotically as the traffic load approaches the system capacity. In contrast, this paper establishes the somewhat surprising result that, when only the first moment of the arrival distribution is known, the error in optimal mean delay due to uncertainties in the arrival model is unbounded as the traffic approaches the system capacity. However, when both first and second moments are known, the error vanishes asymptotically. Numerical examples corroborating the theoretical results are also presented.
Similar content being viewed by others
References
Kleinrock, L.,Queueing Systems, Vol. 1, John Wiley, New York, New York, 1975.
Kumar, A., andBonomi, F.,Adaptive Load Balancing in a Multiprocessor System with a Central Job Scheduler, Proceedings of the 2nd International Workshop on Applied Mathematics and Performance/Reliability Models of Computer Communication Systems, Rome, Italy, pp. 173–188, 1987.
Tsitsiklis, J. N., andBertsekas, D. P.,Distributed Asynchronous Optimal Routing in Data Networks, IEEE Transactions on Automatic Control, Vol. 31, pp. 325–332, 1986.
Gallager, R. G.,A Minimum Delay Routing Algorithm Using Distributed Computation, IEEE Transactions on Communications, Vol. 23, pp. 73–85, 1977.
Chang, F., andWu, L.,An Optimal Adaptive Routing Algorithm, IEEE Transactions on Automatic Control, Vol. 31, pp. 690–700, 1986.
Mohanty, B., andCassandras, C. G.,The Effect of Model Uncertainty on Some Optimal Routing Problems, Journal of Optimization Theory and Applications, Vol. 77, pp. 256–290, 1993.
Ho, Y. C., andCao, X. R.,Perturbation Analysis of Discrete-Event Dynamic Systems, Kluwer Academic Publishers, Boston, Massachusetts, 1991.
Glasserman, P.,Gradient Estimation via Perturbation Analysis, Kluwer Academic Publishers, Boston, Massachusetts, 1991.
Glynn, P.,Likelihood Ratio Gradient Estimation: An Overview, Proceedings of the 1987 Winter Simulation Conference, pp. 336–375, 1987.
Reimann, M., andWeiss, A.,Sensitivity Analysis for Simulations via Likelihood Ratios, Operations Research, Vol. 37, pp. 830–844, 1989.
Bertsekas, D., andGallager, R.,Data Networks, Prentice-Hall, Englewood Cliffs, New Jersey, 1987.
Cassandras, C. G., Abidi, M. V., andTowsley, D.,Distributed Routing with Online Marginal Delay Estimation, IEEE Transactions on Communications, Vol. 38, pp. 348–359, 1990.
Simha, R.,Optimization of Resource Control in Communication Systems, PhD Thesis, University of Massachusetts, Amherst, Massachusetts, 1990.
Ni, L. M., andHwang, H.,Optimal Load Balancing in a Mulitple Processor with Many Job Classes, IEEE Transactions on Software Engineering, Vol. 11, pp. 491–496, 1985.
Tantawi, A. N., andTowsley, D.,Optimal Static Load Balancing in Distributed Computer Systems, Journal of the ACM, Vol. 32, pp. 445–465, 1985.
Buzen, J. P., andChen, P. P. S.,Optimal Load Balancing in Memory Hierarchies, Information Processing, North Holland, Amsterdam, Holland, pp. 271–275, 1974.
Dowdy, L., andFoster, D.,Comparative Models of the File Assignment Problem, ACM Computing Surveys, Vol. 14, pp. 267–314, 1982.
Wah, B.,File Placement in Distributed Computer Systems, IEEE Computer, Vol. 17, pp. 23–33, 1984.
Buzacott, J. A., andShanthikumar, J. G.,Stochastic Models of Manufacturing Systems, Prentice-Hall, Englewood Cliffs, New Jersey, 1992.
Shaked, M., andShanthikumar, J. G.,Stochastic Convexity and Its Applications, Advances in Applied Probability, Vol. 20, pp. 427–446, 1988.
Suri, R.,Robustness of Queueing Network Formulas, Journal of the ACM, Vol. 30, pp. 564–594, 1983.
Cox, D. R., andIsham, V.,Point Processes, Chapman and Hall, London, England, 1980.
De Bruijn, N. G.,Asymptotic Methods in Analysis, North-Holland, Amsterdam, Holland, 1961.
Author information
Authors and Affiliations
Additional information
Communicated by Y. C. Ho
This work was supported by the National Science Foundation under Grants ECS-88-01912 and EID-92-12122 and by NASA under Contract NAG 2-595.
The authors wish to thank an anonymous referee for pointing out Ref. 20, thus avoiding the need for an explicit proof of convexity of the cost function considered in the paper.
Rights and permissions
About this article
Cite this article
Mohanty, B., Cassandras, C.G. Asymptotic analysis of the effect of arrival model uncertainties in some optimal routing problems. J Optim Theory Appl 86, 199–222 (1995). https://doi.org/10.1007/BF02193467
Issue Date:
DOI: https://doi.org/10.1007/BF02193467