Three-dimensional non-isothermal extrusion flows

Abstract

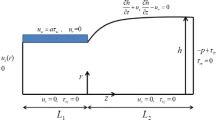
A three-dimensional (3-D) non-isothermal study of viscous free-surface flows with exponential dependence of viscosity on temperature is presented. The effects of non-isothermal conditions and/or geometry on the extrudate shape are investigated with a fully three-dimensional finite element/Galerkin formulation. Apart from the well known thermally induced extrudate swelling phenomenon, bending and distortion of the extrudate may occur because of temperature differences and/or geometric asymmetries. A temperature difference across the die can be imposed by heating or cooling the die walls, but can also arise because of asymmetric viscous heat generation due to the die geometry. Temperature differences affect velocity profiles because of the temperature dependence of viscosity and lead to extrudate bending, an effect known as “kneeing” in the fiber spinning industry. It is also shown numerically and confirmed experimentally that the die geometry induces extrudate bending even in the case of isothermal Newtonian flows.