Cryptanalysis of the FLIP Family of Stream Ciphers

Abstract

At Eurocrypt 2016, Méaux et al. proposed FLIP, a new family of stream ciphers intended for use in Fully Homomorphic Encryption systems. Unlike its competitors which either have a low initial noise that grows at each successive encryption, or a high constant noise, the FLIP family of ciphers achieves a low constant noise thanks to a new construction called filter permutator.

In this paper, we present an attack on the early version of FLIP that exploits the structure of the filter function and the constant internal state of the cipher. Applying this attack to the two instantiations proposed by Méaux et al. allows for a key recovery in $2^{54}$ basic operations (resp. $2^{68}$), compared to the claimed security of $2^{80}$ (resp. $2^{128}$).

Partially supported by the French Agence Nationale de la Recherche through the BRUTUS project under Contract ANR-14-CE28-0015 and by the Commission of the European Communities through the Horizon 2020 program under project number 645622 PQCRYPTO.

1 Introduction

One of the challenges of recent years is to create an acceptable system of Fully Homomorphic Encryption (FHE) that would allow users to delegate computations to so-called Cloud Services. While Gentry showed in [6] the theoretic feasibility of such a framework, two main difficulties remain: first, the important computational and memory costs, and second the limited homomorphic capacities.

In order to overcome these limitations, one of the important aspects that have to be lessened is the cost of the evaluation of the symmetric encryption algorithm used in the framework, which mainly depends on the multiplicative depth of the circuit implementing the primitive. Since adapting the AES seems hard [3, 4, 7], several new symmetric schemes purposed for FHE have been proposed, among which the block cipher LowMC [1] and the stream ciphers Trivium and Kreyvium [2].

At Eurocrypt 2016, Méaux et al. [12] proposed the new stream cipher construction FLIP which aims at overcoming some of the drawbacks of previous schemes by, among other things, allowing for constant and smaller noise. This achievement was made possible by the use of a new construction that resembles a filter generator but with a constant register that is permuted before entering the filtering function in order to limit the multiplicative depth of the circuit.

This design has been presented in October 2015 by the authors of FLIP at a national workshop [11], and then submitted to Eurocrypt 2016. Our study shows that the concrete instantiations proposed by the designers suffer from several flaws that can be extended to a cryptanalysis. We reported our findings to the authors which led them to change their design after their paper was accepted, in order to resist our attack. A fixed version of the construction is then described in the final version of the Eurocrypt 2016 article entitled Toward Stream Ciphers for Efficient FHE with Low-Noise Ciphertexts [12].

In the following, we only deal with the preliminary version of the FLIP family of stream ciphers: so everytime that we mention “FLIP ” we mean the version presented in [11] and submitted to Eurocrypt 2016 (which differs from the final version of [12]).

This paper is organised as follows. We start by giving a description of the submitted version of the FLIP family of stream ciphers in Sect. 2. Then, we discuss its vulnerabilities against guess-and-determine attacks in Sect. 3 and show how to break the cipher by exploiting these vulnerabilities through an algebraic attack (Sect. 4). The pseudocode of the attack is given in Sect. 5. Our analyses are supported by experiments reported in Sect. 6. The last section concludes this paper.

2 Description of the FLIP Family of Stream Ciphers

2.1 General Idea: The Filter Permutator Structure

When it comes to designing a symmetric construction tailored for FHE applications, both block and stream ciphers can be considered, each with advantages and disadvantages, as discussed in [2].

Since the targeted applications use noise-based cryptography (such as lattice-based cryptography), one of the pursued goals is to limit the growth of noise as much as possible, which is equivalent to considering circuits with a limited multiplicative depth. This desirable property, also refered to as a high homomorphic capacity, is hard to obtain with block ciphers since the round iterations lead to an output with a large algebraic degree. However, the good point is that the noise is constant per block, which implies that noise does not add any limitation on the number of generated ciphertext blocks. On the other hand, the homomorphic capacity of stream ciphers is usually very high for the first ciphertext bits, but decreases as more bits are generated, imposing to re-initialise the cipher or to use techniques like bootstrapping.

The innovative design of Méaux et al. [12] succeeds in taking the best from both sides and enjoys a very good homomorphic capacity that remains constant with time. Their proposal is a family of stream ciphers named FLIP that is based on the filter generator construction, but drops the register update part to avoid the algebraic degree increase. Instead, the register bits are permuted before entering the filter function, thus the name filter permutator.

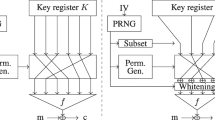
Its operational principle is represented in Fig. 1.

Fig. 1.

General structure of the filter permutator construction used for the FLIP family of stream ciphers.

It is made up of three main components:

• a register storing the N-bit key K,

• a bit permutation generator, parametrised by a public PseudoRandom Number Generator (PRNG), producing at each clock i an N-bit permutation $P_i$,

• a filtering (Boolean) function F, generating the keystream bit $z_i$.

Once the PRNG is initialised using an IV, the master key K is loaded into the register and encryption starts: at each step i, the permutation generator produces a permutation $P_i$ that shuffles the key bits right before they enter the filtering function F. F produces the keystream bit $z_i$ which is XORed to the corresponding plaintext bit $p_i$ and gives the ciphertext $c_i$.

To recover the plaintext, the same process is used to generate the bits $z_i$ of the keystream that are simply XORed back with the $c_i$.

Every part of the scheme is public except the key.

2.2 The FLIP Family of Stream Ciphers

After an extensive analysis of the filter permutator construction with respect both to FHE constraints and resistance against most common stream ciphers attacks, the authors chose the concrete instantiation we now describe.

The PRNG used for the permutation generator is defined as a forward secure PRNG based on AES-128, and the permutation generator itself is a Knuth shuffle [9], which ensures that all the N-bit permutations have the same probability to be generated (provided that it is used with a random generator).

F is an N-variable Boolean function defined by the direct sum of three specific Boolean functions $f_1$, $f_2$ and $f_3$ that are defined in [13] and that we now recall.

In the following, n and k are positive integers and operations are considered over $\mathbb {F}_2$.

Definition 1

(L-type Function). The n-th L-type function $L_n$ is the n-variable linear function defined by:

$$\begin{aligned} L_n(x_0, \cdots , x_{n-1})=\sum _{i=0}^{n-1} x_{i}. \end{aligned}$$

Definition 2

(Q-type Function). The n-th Q-type function $Q_n$ is defined by the 2n-variable quadratic function:

$$\begin{aligned} Q_n(x_0, \cdots , x_{2n-1})=\sum _{i=0}^{n-1} x_{2i}x_{2i+1} \end{aligned}$$

Definition 3

(T-type Function). The k-th T-type function is the $\frac{k(k+1)}{2}$-variable Boolean function defined by:

$$\begin{aligned} T_k(x_0, \cdots , x_{ \frac{k(k+1)}{2} - 1 }) = \sum _{i=1}^{k} \prod _{j=0}^{i-1} x_{j+\sum _{\ell =0}^{i-1}\ell }. \end{aligned}$$

For instance the 3rd T-type function is equal to:

$$\begin{aligned} T_3 = x_0+ x_1x_2 + x_3x_4x_5 \end{aligned}$$

Each of these types of functions has nice properties according to one or several security criteria (non-linearity, resiliency, algebraic immunity, $\ldots$).

The filtering function used in the FLIP family of stream ciphers uses a combination of 3 Boolean functions parameterised by the integers $n_1$, $n_2$ and $n_3$, chosen so that the resulting properties of F are good:

• $f_1(x_0,\cdots , x_{n_1-1}) = L_{n_1}$,

• $f_2(x_{n_1},\cdots , x_{n_1+n_2-1}) = Q_{n_2/2}$,

• $f_3(x_{n_1+n_2},\cdots , x_{n_1+n_2+n_3-1}) = T_{k}$ where k is such that $n_3 = \frac{k(k+1)}{2}.$

F is defined as the direct sum of $f_1$, $f_2$ and $f_3$:

$$F(x_0, \cdots , x_{n_1+n_2+n_3-1}) = L_{n_1} + Q_{n_2/2} + T_{k} ~~ \text {where } n_1+n_2+n_3 = N$$

and thus inherits in some measure the good properties of $f_1$, $f_2$ and $f_3$ (see [13]).

The initial analysis performed by Méaux et al. and presented in the submitted version of the construction [13] takes into account the most common attacks on filter generators (which are very similar to filter permutators) and resulted in the selection of the parameters reported in Table 1.

Table 1. Parameters of the two concrete instantiations of FLIP with the corresponding complexities of Algebraic Attacks (AA), Fast Algebraic Attacks (FAA) Higher-Order Correlation attacks (HC).

The security analysis detailed in [13] and more precisely the study of weak keys results in an additional limitation on the design which is that the key must be balanced (in the submitted version of the Eurocrypt paper [13] it is stated that: “Since our N parameter will typically be significantly larger than the bit-security of our filter permutator instances, we suggest to restrict the key space to keys of Hamming weight N / 2").

Finally, note that the specification document does not give any limit on the number of keystream bits that can be generated under the same key.

3 Preliminary Remarks on the Vulnerabilities of the FLIP Family of Stream Ciphers

3.1 Attack Scenario and Computation Model

In the following we examine one of the most common attack scenarios considered for stream cipher analysis, which is the known-plaintext scenario: we suppose that we know a part of the plaintext together with the corresponding ciphertext, which implies that we know the value of some bits of the keystream z. Needless to say, our goal is to recover the secret key, which in the case of the FLIP family of stream ciphers is equivalent to recovering the internal state.

To express the performance of our attack, we use the three usual metrics which are time, data and memory complexities. Time complexity (hereafter denoted by $C_T$) expresses the quantity of operations that the attacker has to perform to execute the attack. In our case, we compute it in the same way as in the specification paper [13] so we count the number of basic operations. Data complexity ($C_D$) corresponds to the required number of keystream bits and finally memory complexity ($C_M$) measures the memory (in bits) needed during the attack.

3.2 The FLIP Family of Stream Ciphers and Guess-and-Determine Attacks

The attack we propose uses a variant of the guess-and-determine technique. This approach, which seems to have been named first in [5, 8], has been extensively used to analyse stream ciphers, starting with the ones submitted to the NESSIE project. The idea is to start by making a hypothesis on the value of some bits of the internal state or of the key (the ‘Guess’) and to use the information coming from keystream bits to deduce the unknown ones (to ‘Determine’ them). Most of the time the attack is completed thanks to algebraic techniques.

Two features of the FLIP family of stream ciphers seem to indicate that an attack using guess-and-determine techniques would be efficient: first its fixed internal state and second the definition of its filtering function. More precisely, the fact that the register is not updated implies that a guess of one key/internal state bit at any time would give an information of one bit at any other time. This is different from common stream ciphers for which the update function mixes the internal state bits together, implying that a one-bit information quickly vanishes after some (forward or backward) rounds.

The second feature that seems exploitable for a guess-and-determine attack is the definition of the filtering function F which contains very few monomials of high-degree. This is what we detail now.

3.3 Observations on the Boolean Function F

As reported before, the Boolean function F is made of the direct sum of 3 Boolean functions $f_1$, $f_2$ and $f_3$ which are respectively of L-, Q- and T-type. This definition implies that all the monomials of degree greater than or equal to 3 are present in $f_3$, which is given by the following formula:

$$\begin{aligned} f_3(x_{n_1+n_2},\cdots , x_{n_1+n_2+n_3-1})= & {} T_{k}(x_{n_1+n_2},\cdots , x_{n_1+n_2+n_3-1}) \\= & {} \sum _{i=1}^{k} \prod _{j=n_1+n_2}^{n_1+n_2+i-1} x_{j+\sum _{\ell =0}^{i-1}\ell } \end{aligned}$$

where k is the algebraic degree of $f_3$ and is such that $n_3 = \frac{k(k+1)}{2}.$

From this expression, we see that there are $k-2$ monomials of degree greater than or equal to 3 in F, in a total of $n_3-3$ variables. Given the multiplicative depth constraint, k has to be low¹, which implies that the T-type function has few monomials and therefore easy to cancel, as we show in the next section.

The core idea of our attack is to notice that since there are few high-degree monomials but a lot of null key bits, there is a high probability that the high-degree monomials of F are cancelled. In these cases, it also means that the keystream bits can be seen as expressions of degree less than or equal to 2  in the non-null key bits.

The attack we perform uses this specificity by doing a slight variant of the guess-and-determine technique: instead of making a hypothesis on the value of key/internal state bits, we guess the indices of some null key bits². We deduce from that the clocks when the keystream bits are an expression of low-degree in the other key bits and build a system from it. Finally we solve the system with linearisation techniques, which in the case of low-degree equations is of reasonable cost.

3.4 Probability of Cancelling all the High-Degree Monomials of F Given that $\ell$ Input Variables are Null

To figure out the feasibility of such a procedure, we have to evaluate the probability that, given exactly $\ell$ positions of null bits in K, the expression of the keystream bit $z_i$ is of degree less than or equal to 2  in the remaining key bits³.

This probability is directly linked to the amount of data that is required to lead to the attack since it determines the amount of keystream bits that an attacker needs such that enough of them are exploitable to construct the system.

From the previous discussion, we know that there are exactly $k-2$ disjoint monomials of degree greater than or equal to 3  in the expression of $z_i = F( P_i(k_0, k_1, \cdots k_{N-1}) )$. Then, if the attacker is only aware of $\ell < k-2$ zero positions, she won’t be able to determine exploitable clocks, which forces $\ell \ge k-2$, i.e. at minimum one zero bit that could be positioned in each of the high-degree monomials.

First case: if $\pmb {\ell = k-2}$ . The first possibility is to choose the number of null positions equal to the number of high-degree monomials that we want to cancel, i.e. $\ell = k-2$. In this case, exactly one null bit has to go into each monomial: for instance, if we are looking at a specific monomial of degree d: $x_0x_1 \cdots x_{d-1}$, it is equivalent to choosing which of the variables is null, so there are d possibilities. From that, we can enumerate the set of valid configurations, which corresponds to choosing one index in each monomial, so since there are 3 possible choices for the monomial of degree 3, 4 possibilities for the one of degree 4 and so on up to the monomial of degree k, there is a total of $3\times 4\times 5 \cdots \times k = k!/2$ valid configurations. To obtain the probability, this amount has to be compared with the total number of possibilities for choosing the null positions, which is ${N \atopwithdelims ()\ell }$ so we have:

$$\mathbb {P}_{\ell = k-2} = \frac{k!/2}{ {N \atopwithdelims ()\ell } }.$$

General case: if $\pmb {\ell \ge k-2}$ . To increase the probability that a clock is exploitable, the attacker can guess more null key bit positions and choose $\ell \ge k-2$. A first way of computing this probability is:

$$\mathbb {P}_{\ell }=\frac{\sum _{i_1+i_2+\cdots +i_{k-2}\le \ell } {3 \atopwithdelims ()i_1} {4 \atopwithdelims ()i_2} \cdots {k \atopwithdelims ()i_{k-2}} {N-m \atopwithdelims ()\ell -I} }{{N \atopwithdelims ()\ell }}$$

where m is the number of variables that occur in the monomials of degree greater than or equal to 3 and $I=i_1+i_2+\cdots +i_{k-2}$.

Proof

Suppose that we are given $\ell$ null bit positions in K. We are interested in the probability that a random permutation $P_i$ shuffles the key bits in a way that the evaluation of F does not contain any monomial of degree greater than or equal to 3. As previously, we count the number of valid configurations among the total number of permutations.

The idea is to list all the possible ways of positioning at least one null bit in each monomial: we set $i_1$ null bits in the monomial of degree 3, $i_2$ null bits in the monomial of degree 4, and so on up to $i_{k-2}$ null bits in the monomial of highest degree (k). If we denote by $I=i_1+i_2+\cdots +i_{k-2}$ the number of null bits positioned in such a way, we are left with $\ell -I$ null bits to position in the other $N-m$ monomials. To obtain the probability, we have to divide this quantity by the number of ways to position $\ell$ guesses among N bits.    $\square$

Another way of obtaining the probability is to compute the number of configurations that do not cancel the monomials of degree greater than or equal to 3, which is the complementary probability of the one we are looking for. The advantage is that this complementary can be easily expressed with the inclusion-exclusion principle. Let us denote $A_{J}$ the event that our guess doesn’t cancel the monomials of degrees included in the set J, i.e.

$$A_J \text { is the event: } \{\forall j\in J,\, M_j \ne 0\}$$

where $M_j$ is the unique monomial of degree j in $T_k$.

$\mathbb {P}(A_J)$ is the probability of setting the $\ell$ bits among the monomials whose degrees are not in J so is equal to:

$$\mathbb {P}(A_J) = \frac{{{N-\sum \limits _{j\not \in J} j}\atopwithdelims ()\ell }}{{N \atopwithdelims ()\ell }}$$

Then we can express the probability that our guess yields a polynomial of degree higher than or equal to 3 by:

$$\mathbb {P}(\bigcup _{d\in \{3,\cdots ,k\}} A_{\{d\}}) = \sum \limits _{s=1}^{k-2} \bigg ((-1)^s\sum \limits _{\begin{array}{c} J\subseteq \{3,\cdots ,k\} \\ |J|=s \end{array}} \mathbb {P}(A_J)\bigg )$$

which can be expressed as

$$\mathbb {P}(\bigcup _{d\in \{3,\cdots ,k\}} A_{\{d\}}) = \frac{\sum \limits _{s=1}^{k-2} \bigg ((-1)^s\sum \limits _{\begin{array}{c} J\subseteq \{3,\cdots ,k\} \\ |J|=s \end{array}} {{N-\sum \limits _{j\not \in J} j}\atopwithdelims ()\ell }\bigg )}{{N \atopwithdelims ()\ell }}$$

From which we get the expression of the probability that we are looking for:

$$\mathbb {P}_{\ell } = \mathbb {P}(\bigcap _{d\in \{3,\cdots ,k\}} \overline{A_{\{d\}}}) = 1 - \mathbb {P}(\bigcup _{d\in \{3,\cdots ,k\}} A_{\{d\}})$$

The evaluation of these formulas gives the results reported in Tables 3, 4 and 5 in Appendix, and we will see in the next section that they are good enough to mount an attack. For instance, if we attack the small version⁴ of FLIP and do the minimal number of guesses (i.e. $\ell = 12$) we will have a probability of having an exploitable equation of $\mathbb {P}_{\ell = 12} = 2^{-26.335}$. For the other version⁵ and a minimal number of guesses we have $\mathbb {P}_{\ell = 19} = 2^{-42.382}$.

4 Our Attack

4.1 Description

Setting. Since we consider a known-plaintext scenario, we suppose that we are given $C_D$ keystream bits that we denote by $z_i$, $i=0, \cdots , C_D-1$. Additionally, the associated permutations $P_i$ are public so we have expressions of the keystream bits as function of the unknown key bits $k_0, \cdots , k_{N-1}$:

$$\begin{aligned} z_i = F( P_i(k_0, k_1, \cdots , k_{N-1}) )~~~ \forall i\ge 0 \end{aligned}$$

Our attack takes advantage of the two vulnerabilities detailed in the previous section to boil down the key recovery problem to the solving of a linearised system.

First step: initial guess. The first step consists in making a hypothesis on the positions of $\ell$ null key bits, where $\ell \ge k-2$. Assuming that these bits are null gives us a simplified expression of $z_i$ in only $N-\ell$ unknowns. Since the key K is balanced, the probability of our guess being right is⁶:

$$\begin{aligned} \mathbb {P}_{rg} = \frac{{{\frac{N}{2} \atopwithdelims ()\ell }}}{{{N \atopwithdelims ()\ell }}} \end{aligned}$$

Second step: extraction of low-degree equations. The objective of step 2 is to collect equations of low-degree in the unknown key bits. To do so, we look at the expressions of the available $z_i$ and pick up all the equations for which the null key bits cancel the monomials of degree greater than or equal to 3. As seen in previous section, this event is of probability $\mathbb {P}_{\ell }$.

Third step: solving the system. One of the easiest ways of solving the quadratic system is to use linearisation techniques, which consist in converting the system into a linear one by introducing a new variable for each non-linear monomial that appears. In our specific case, the only non-linear expressions we have to deal with are the monomials of degree 2. Since F takes as input N variables but we guessed $\ell$ of them, we are left with $N-\ell$ unknown variables, which in the worst case scenario form ${N-\ell \atopwithdelims ()2}$ monomials of degree two. This implies that once linearised, our converted system will contain

$$v_{\ell } = N - \ell + {N-\ell \atopwithdelims ()2}$$

variables.

Assuming that the equations are random, the number of equations that are necessary to give a unique solution (or show a contradiction) is roughly equal to the number of unknowns⁷. This implies that the necessary amount of keystream bits that the attacker needs is the product of the number of variables and the inverse of the probability that a $z_i$ is exploitable:

$$C_D = v_{\ell } \times \frac{1}{\mathbb {P}_{\ell }}$$

The time complexity is determined by the time to solve the system⁸ multiplied by the number of times we have to repeat the guess of $\ell$ null bit positions before finding a correct one:

$$C_T = v_{\ell }^3 \times \frac{1}{\mathbb {P}_{rg}}$$

The final memory complexity is dominated by the memory necessary to store the system, so is roughly equal to:

$$C_M = v_{\ell }^2 $$

Tables 3, 4 and 5 in Appendix give the possible trade-offs between time and data complexity for the two versions of FLIP. As we can see, increasing the number of initial guesses $\ell$ allows to reduce the amount of data necessary to conduct the attack at the cost of an increased time complexity.

4.2 Discussion and Possible Improvements

Data Complexity Reduction. The data complexity can be further improved if, rather than choosing the guesses at random, the attacker chooses them according to the observed permutations. With the PRNG seed being public, at any point in time, she knows all the upcoming permutations so she can deduce a guess that cancels the triangular part for many of the upcoming permutations.

Possibility of Precomputations. Most of the computational cost of the attack lies in the linear system solving. Notice that this linear system depends only on the permutation and the guess, which are all known to the attacker, who can therefore compute the system inversion for several guesses without any knowledge of the keystream. Once she receives the keystream bits, she plugs them into her precomputations to obtain the results. The drawback of this technique is its increase in memory complexity.

Seed Independence. Our attack has the property of being unaffected by a re-initialisation of the system. What we mean here is that a change of the PRNG seed in the middle of the attack will not force the attacker to restart her attack: she can combine the previously obtained equations with the one obtained under the new seed.

Security. The security level of the FLIP family of stream ciphers is at most proportional to $\sqrt{N}$ bits, where N is the key size.

Proof

The time complexity of our attack is

$$C_T=v_{\ell }^3 \times \frac{1}{\mathbb {P}_{rg}}$$

As $\ell \ll N$, one can say that $\mathbb {P}_{rg}$ is roughly equivalent to $2^{-\ell }$. Also, as $v_\ell = N-\ell +{N-\ell \atopwithdelims ()2}$, we can give an approximation of $C_T$ which is

$$C_T\sim N^6\times 2^\ell $$

Additionally, the number of guesses we need to perform our attack is the number of monomials of degree greater than or equal to 3 in $T_{n_3}$. Thus $n_3 = (\ell +2)(\ell +3)/2$, so $\ell \sim \sqrt{n_3}$, from which we get:

$$\log {C_T}\sim \alpha \sqrt{N}$$

   $\square$

Figure 2 represents the evolution of the time complexity of our attack as function of the key size when we consider instances of FLIP of the form FLIP  $(n_1,n_2,n_3)$ where $N = n_1+n_2+n_3 = 2n_3$ (which is consistent with the parameters proposed in [13]). $\ell$ is chosen as the minimal number of guesses needed to perform the attack, i.e. $\ell = k-2$.

Fig. 2.

Evolution of the time complexity as function of the key size N.

Attempt to Cancel the Quadratic Part. Our attack consists in guessing key bits to cancel the triangular part of the filtering function: another possibility would be to cancel the monomials of degree 2  in order to reduce the resistance of the scheme against correlation attacks. We considered this option but our studies showed that the complexity of such an attack would be too high. We also thought of cancelling both quadratic and triangular parts, thus leaving only linear relations, but the data complexity of such an attack makes it less practical.

5 Description of the Algorithm

The main computation part of our attack is a linear system solving over $\mathbb {F}_2$. If the solving detects a contradiction, we deduce that our guess is wrong and we start again with another guess. Otherwise, the guess was right and the solving yields the key. The intuition is that we don’t always need a full-rank system to detect a contradiction. We can therefore improve the attack by treating every equation as they come, rather than waiting for a full-rank system.

A pseudocode description of the attack using this improvement is given in Algorithm 1. In this algorithm, an equation will be represented as a $(v_\ell +1)$-bit word containing 1 where a variable is present in the equation and 0 otherwise. The least significant bit of this representation contains the value of the keystream bit of the equation. We also memorise if equation i is present in the system through the vector Exists. If $Exists[i]=1$, then equation i is in the system.

6 Verification of the Attack on a Toy Version

To support our findings, we implemented our attack on a toy version of the cipher. We reduced the key size to $N = 64$ bits and adapted accordingly the values of the parameters to $n_1 = 14$, $n_2 = 14$ and $n_3 = 36$ (the proportions between the size of the parameters are kept). The filtering function F has algebraic degree 8 and is defined as follows:

$$\begin{aligned} F(x_0, \cdots x_{63}) = f_1(x_0,\cdots x_{13}) + f_2(x_{14}, \cdots x_{27}) + f_3(x_{28}\cdots x_{63}) \end{aligned}$$

where:

According to our analysis, the parameters of the attacks are the ones described in Table 6: for instance if we decide to make a hypothesis on $\ell =8$ null indices, the probability that our guess is correct is

$$\mathbb {P}_{rg} = 2^{-8.717}.$$

The probability that a permutation is exploitable is equal to:

$$\mathbb {P}_{\ell } = 2^{-7.814}$$

and the linearised system depends on $v_\ell = 1596$ variables. We expect that $C_D = 2^{18.454}$ bits are necessary to conduct the analysis and that the attack requires $C_T = 2^{40.638}$ basic operations.

Table 2. Comparison of the experimental results with theory: attack on the toy version FLIP  (14,14,36) with a hypothesis on $\ell = 8$ null bit positions (average on 1000 tests, launched on an Intel(R) Xeon(R) CPU W3670 at 3.20 GHz (12 MB cache), and with 8 GB of RAM)

We implemented our own version of this toy instance of FLIP on which we performed our attack with $\ell =8$ guesses. The statistics we obtain are given in Table 2.

Although the equations have a very specific structure, we noticed that they behave like random equations in the following sense: the first linearly dependent equation is only found after generating 1590 equations, which fits with the theory in the case of random equations [10]. However, treating the equations as they come allows us to discard right away any equation that is linearly dependent from the others. This way, we can stop collecting equations as soon as we have as many equations in our system as are variables⁹.

As we can see in Table 2, experimental results fit pretty well with the theory.

7 Conclusion

In this paper we presented a cryptanalysis of the FLIP family of stream ciphers. Our attack makes use of the weaknesses of the FLIP structure against guess-and-determine attacks to reduce the degree of the filtering function, after what an algebraic attack suffices to recover the key. We obtained theoretical estimations of the complexity of the attack and an implementation of the attack on a toy version shows that this complexity holds in practice. This attack can be performed in $2^{54}$ basic operations (resp. $2^{68}$), compared to the claimed security of $2^{80}$ (resp. $2^{128}$), and we discussed trade-offs and improvements that can lower this complexity even more. We also underlined that a simple increase of the key size is not an efficient countermeasure as the complexity of the attack doesn’t increase much with the key size.

Finally, in view of fixing this attack, one should keep in mind the inherent weakness of the filter permutator construction against guess-and-determine attacks due to its constant register. The biggest issue of the FLIP family of stream ciphers is that its filtering function increases the fragility against guess-and-determine attacks. To strengthen the security of the filter permutator, a possible direction would be to refine its filtering function, for instance by using more high-degree monomials.

A  Possible Trade-Offs

A.1  FLIP (47,40,105)

See Table 3.

Table 3. Log of the complexities of the attacks as function of the number of initial guesses ($\ell$) for the instantiation FLIP (47,40,105)

A.2  FLIP (87,82,231)

See Tables 4 and 5.

Table 4. Log of the complexities of the attacks as function of the number of initial guesses ($\ell$) for the instantiation FLIP (87,82,231)

Table 5. Log of the complexities of the attacks as function of the number of initial guesses ($\ell$) for the instantiation FLIP (87,82,231)

B  Complexities of the Attack on the Toy Version of FLIP

See Table 6.

Table 6. Log of the complexities of the attacks as function of the number of initial guesses ($\ell$) for the toy version FLIP (14,14,36)