2D-3D Registration Accuracy Estimation for Optimised Planning of Image-Guided Pancreatobiliary Interventions

Abstract

We describe a fast analytical method to estimate landmark-based 2D-3D registration accuracy to aid the planning of pancreatobiliary interventions in which ERCP images are combined with information from diagnostic 3D MR or CT images. The method analytically estimates a target registration error (TRE), accounting for errors in the manual selection of both 2D- and 3D landmarks, that agrees with Monte Carlo simulation to within 4.5 ± 3.6 % (mean ± SD). We also show how to analytically estimate a planning uncertainty incorporating uncertainty in patient positioning, and utilise it to support ERCP-guided procedure planning by selecting the optimal patient position and X-ray C-arm orientation that minimises the expected TRE. Simulated- and derived planning uncertainties agreed to within 17.9 ± 9.7 % when the root-mean-square error was less than 50°. We demonstrate the feasibility of this approach on clinical data from two patients.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

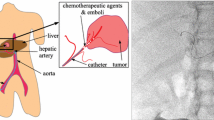
Endoscopic retrograde cholangiopancreatography (ERCP) is an imaging technique that provides real time, planar X-ray images of the bile ducts following the intra-ductal injection of a radio-opaque contrast agent via a catheter. It is the standard guidance technique for many diagnostic and therapeutic endoscopic interventions involving the pancreatobiliary ducts, such as ductal lesion tissue sampling and stenting, where it is used to navigate catheter-based instruments through the ductal tree. As ERCP-guided procedures can be technically demanding with a significant risk of complications, such as post-procedural pancreatitis (2–16 %) and cholangitis (<1%) [1], there is growing clinical interest in using high-quality 3D CT and MR imaging of the pancreatobiliary system to plan interventional procedures and to enhance the navigational information provided by ERCP. For example, a 3D graphical representation of organs such as the pancreas, the biliary tree, and associated pathology (such as cysts and cancerous lesions) obtained from an MR or CT scan; might be displayed together with an indication of the current 3D location of instruments determined from ERCP images during a procedure. Alternatively, anatomical structures and landmarks defined within the MR/CT scan can be displayed superimposed on ERCP images by projecting these onto the X-ray plane. Adopting multimodal image guidance using either of these approaches has the potential advantages of increasing surgical accuracy and confidence, and reducing the technical skill and time required to perform a procedure. Such benefits are likely to be especially useful in enabling rapid localisation of pathology in the more distal biliary tree, and in cases where strictures prevent or severely impede the visualisation of the bile ducts more distal to the ampulla of Vater. Enhanced surgical guidance also offers the potential to reduce the risk of ERCP-contrast-related toxicity and radiation dose by reducing the reliance on ERCP for visualisation of the ductal tree.

A fundamental requirement of multimodal image guidance is the registration of ERCP and MR/CT images. This is a 2D-3D image registration problem, solutions for which have been the subject of a substantial body of research, although largely in the context of other applications, such as orthopaedic surgery and neurovascular interventions [2]. Very few studies have focused on multimodal image guidance for ERCP-guided pancreatobiliary interventions; in [3, 4], for example, commercial guidance systems were used to guide radiosurgery of pancreatic cancer, with registration achieved by matching implanted fiducials. However, the use of implanted fiducials specifically for registration is in general very difficult to justify for the majority of patients undergoing ERCP-guided procedures. For this reason, in this work we focus on registration using anatomical landmarks.

The ability to predict intraoperative registration accuracy is becoming increasingly important as guidance systems become more widely adopted in clinical practice. For ERCP-guided pancreatobiliary procedures this information could be used to optimise registration protocols, for example, by informing the selection of anatomical landmarks so that a sufficient number of landmarks are used, with an adequate geometric configuration, to ensure an accurate registration. Furthermore, predicted registration accuracy can inform how much confidence a clinician should place in a 3D guidance system, determining whether additional effort should be made to improve a registration – for example, changing the position of a C-arm X-ray or searching for additional landmarks in the ERCP image. In this paper, we develop a new, fast analytical method for estimating 2D-3D registration error, with a particular focus on pancreatobiliary procedures, and demonstrate how it can be applied practically to predict and optimise landmark-based registration of ERCP and MR cholangiopancreatography (MRCP) images.

2 Analytical Estimation of 2D-3D Registration Error

In this section, we develop an analytical model of error propagation for a landmark-based 2D-3D registration in which corresponding anatomical landmarks defined in both 2D- and 3D images are matched. Figure 1 shows a schematic of the variables and errors involved. The objective of the model is to estimate the target registration error (TRE), given locations of registration landmarks and one or more independent ‘target’ landmarks, both defined in the 3D image; error estimates for these landmarks, referred to here as 3D landmark localisation errors¹ (LLEs); error estimates for registration landmarks defined within the 2D image, 2D LLEs; estimates of the parameters of the transformation that match the 2D- and 3D registration landmarks.

Fig. 1.

A schematic showing the variables and errors involved in registration and planning of an ERCP-guided procedure (see Sects. 2 and 3 for details).

Assuming that the 2D images are produced by projection, as is the case for ERCP, the 2D coordinates of a landmark, defined by the position vector, ${\mathbf{u}} = [u, v]^{T }$, in the 2D image are given by:

$$ {\mathbf{u}} = {\mathbf{f}}_{\text{p}} \left( {{\mathbf{f}}_{\text{r}} \left( {{\mathbf{x}},{\varvec{\uptheta}}} \right),{\mathbf{K}}} \right) $$

(1)

where ${\mathbf{x}} = [x, y, z]^{T }$ is the position vector containing the 3D coordinates of the landmark in the 3D image; ${\mathbf{f}}_{\text{p}}$ is the perspective projection transformation; ${\mathbf{K}}$ is the camera matrix, determined by the focal length (i.e. the distance between the X-ray source and detector) and the principal point coordinates. These 2D imaging parameters are assumed known and well-calibrated; and ${\varvec{\uptheta}} = \left[ {\alpha_{x} ,\alpha_{y} ,\alpha_{z} ,t_{x} ,t_{y} ,t_{z} } \right]^{T}$ is a vector containing the 3 rotation and 3 translation parameters of a rigid-body transformation, ${\mathbf{f}}_{\text{r}}$, which may also be parameterised by a 3 × 3 rotation matrix ${\mathbf{R}}(\alpha_{x} ,\alpha_{y} ,\alpha_{z} )$ and a translation vector ${\mathbf{t}} = \left[ {t_{x} ,t_{y} ,t_{z} } \right]^{T} .$ Rewriting (1) in terms of ${\mathbf{R}}$ and ${\mathbf{t}}$, and using homogenous coordinates with a normalisation scaling factor, $\lambda$, we have:

$$ \lambda \left[ {\begin{array}{*{20}c} {\mathbf{u}} \\ 1 \\ \end{array} } \right] = {\mathbf{K}}\left[ {\begin{array}{*{20}c} {{\mathbf{Rx}} + {\mathbf{t}}} \\ 1 \\ \end{array} } \right]. $$

In this work, registration of the 2D- and 3D images was achieved by minimising a collinearity-based error in 3D (as opposed to 2D) image space using the orthogonal iteration algorithm [5].

Anatomical landmarks used in registration are defined with inherent uncertainties, due to the intra/inter-operator localisation error, anatomical variations, projection-related ambiguity, and tissue motion. Assuming an independent, anisotropic and heterogeneous Gaussian error model, the following errors are involved (see also in Fig. 1): (a) A 3D LLE for the $i^{th} (i = 1, \ldots ,n)$ 3D landmark ${\mathbf{x}}_{i}$, represented by 3D covariance matrix ${\varvec{\Sigma}}_{{{\mathbf{x}}_{i} }}$; (b) a 2D LLE on the corresponding 2D landmark ${\mathbf{u}}_{i}$ represented by 2D covariance matrix ${\varvec{\Sigma}}_{{{\mathbf{u}}_{i} }}$; (c) errors on $m$ transformation parameters ${\varvec{\uptheta}}$ (here, $m = 6$), a 6D covariance matrix ${\varvec{\Sigma}}_{{\varvec{\uptheta}}}$; and, (d) an error, represented by a 3D matrix ${\varvec{\Sigma}}_{{\mathbf{r}}}$, associated with the target of interest, defined in the preoperative image by position vector ${\mathbf{r}}$.

First, we would like to compute the uncertainty in transformation parameter ${\varvec{\uptheta}}$, i.e. ${\varvec{\Sigma}}_{{\varvec{\uptheta}}}$, given uncertainties from both 2D- and 3D LLEs, ${\varvec{\Sigma}}_{{{\mathbf{x}}_{i} }}$ and ${\varvec{\Sigma}}_{{{\mathbf{u}}_{i} }}$. Hoff et al. [6] derived a backward propagation of covariance using a direct least-squares, pseudo-inversion of a full rank Jacobian to estimate ${\varvec{\Sigma}}_{{\varvec{\uptheta}}}$. Sielhorst et al. [7] directly utilised the forward- and backward propagation of covariance, summarised in [8], estimating errors for an optical tracking application. Both of these studies considered only 2D LLEs, i.e. true values of ${\mathbf{x}}_{i}$, the geometry of the calibrated tracking tool, are known without uncertainty. However, this assumption does not hold in 2D-3D registration applications and the registration error should be estimated by considering both ${\varvec{\Sigma}}_{{{\mathbf{x}}_{i} }}$ and ${\varvec{\Sigma}}_{{{\mathbf{u}}_{i} }}$. This can be achieved by modifying Eq. (1) and considering a new vector function:

$$ \left[ {\begin{array}{*{20}c} {\mathbf{u}} \\ {\mathbf{x}} \\ \end{array} } \right] = {\mathbf{f}}_{\text{p}}^{\varvec{*}} \left( {\left[ {\begin{array}{*{20}c} {\varvec{\uptheta}} \\ {\mathbf{x}} \\ \end{array} } \right],{\mathbf{K}}} \right) $$

(2)

in which, the same perspective projection still holds, but the 3D landmarks are now treated as additional parameters to estimate as well as trivial function outputs. The parameter space of ${\mathbf{f}}_{\text{p}}^{\varvec{*}}$ now becomes $m + 3n$ dimensional whilst the function (measurement) space, becomes $2n + 3n$ dimensional. Linearly approximating the vector transformation function ${\mathbf{f}}_{\text{p}}^{\varvec{*}}$ by a first-order Taylor series, a ($2n + 3n) \times (m + 3n)$ Jacobian matrix ${\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{\varvec{*}}$ can be computed to map the $2n + 3n$ dimension covariance matrix ${\varvec{\Sigma}}_{{{\mathbf{U}},{\mathbf{X}}}}$ onto an $m + 3n$ dimension parameter space. Without loss of generality, and assuming independence between the measured landmarks, the new backward propagation formula is:

$$ \widehat{\sum }_{{{\varvec{\uptheta}},{\mathbf{X}}}} = \left( {{\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{*T} {\varvec{\Sigma}}_{{{\mathbf{U}},{\mathbf{X}}}}^{ - 1} {\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{*} } \right)^+$$

(3)

where ${\varvec{\Sigma}}_{{{\mathbf{U}},{\mathbf{X}}}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\varvec{\Sigma}}_{{{\mathbf{u}}_{1} }} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {{\varvec{\Sigma}}_{{{\mathbf{u}}_{n} }} } \\ \end{array} } & 0 \\ 0 & {\begin{array}{*{20}c} {{\varvec{\Sigma}}_{{{\mathbf{x}}_{1} }} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {{\varvec{\Sigma}}_{{{\mathbf{x}}_{n} }} } \\ \end{array} } \\ \end{array} } \right],\,{\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{*} \left( {{\mathbf{u}}_{i} } \right) = \left[ {\frac{{\partial {\mathbf{f}}_{\text{p}} }}{{\partial {\mathbf{u}}_{i} }}} \right]_{{i,{\varvec{\uptheta}}}}^{T} \,{\text{and}}\,{\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{*} \left( {{\mathbf{x}}_{i} } \right) = \left[ {\frac{{\partial {\mathbf{f}}_{\text{p}} }}{{\partial {\mathbf{x}}_{i} }}} \right]_{{i,{\varvec{\uptheta}}}}^{T} .$

The estimated covariance of registration parameters ${{\varvec{\widehat{\Sigma}}}}_{{\varvec{\uptheta}}}$ is the $m \times m$ leading principal submatrix of ${{\varvec{\widehat{\Sigma}}}}_{{{\varvec{\uptheta}},{\mathbf{X}}}}$. The pseudo-inverse operator, applicable when the Jacobian has a rank smaller than the number of columns, is denoted by $( \cdot )^+$.

Given estimated values for ${{\varvec{\widehat{\Sigma}}}}_{{\varvec{\uptheta}}}$, transforming the covariance of an independent target point (i.e. covariance ${\varvec{\Sigma}}_{{{\varvec{\uptheta}},{\mathbf{r}}}} = 0$) at location ${\mathbf{r}}$ is a straightforward application of the forward propagation which maps parameter space onto function space:

$$ \widehat{\sum }_{{{\mathbf{u}}_{{\mathbf{r}}} }} = {\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }} \left( {\varvec{\uptheta}} \right)\widehat{\sum }_{{\varvec{\uptheta}}} {\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{T} \left( {\varvec{\uptheta}} \right) + {\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }} \left( {\mathbf{r}} \right){\varvec{\Sigma}}_{{\mathbf{r}}} {\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{T} \left( {\mathbf{r}} \right) $$

(4)

where ${\mathbf{u}}_{{\mathbf{r}}} = {\mathbf{f}}_{\text{p}} \left( {\mathbf{r}} \right)$ is the projected target point in 2D. A scalar root-mean-square error (RMSE) can also be computed, $TRE = \sqrt {trace\left( {{{\varvec{\widehat{\Sigma}}}}_{{{\mathbf{u}}_{{\mathbf{r}}} }} } \right)}$.

3 Estimation of Planning Error for ERCP-Guided Procedures

In this section, we develop an example framework for planning ERCP-guided procedures that minimises the estimated TRE to optimise patient position and C-arm orientation, for which, an analytical formulation of uncertainty in planning is introduced to assess the optimised plan.

The estimated TRE from Sect. 2 is dependent on the estimates of transformation parameters ${\varvec{\uptheta}}$, which are determined by the physical position of the X-ray positioner and the patient. Over-parameterising ${\mathbf{f}}_{\text{r}}$ in Eq. (1), a point ${\mathbf{x}}_{\text{plan}}$ defined in 3D plan space (i.e. the physical coordinate system of the preoperative image in mm) can be transformed to ${\mathbf{x}}_{\text{pos}}$ in positioner space (the camera or C-arm space, in which the X-ray source is the centre of projection and at the origin, and the detector is parallel to the x-y plane). One possible parameterisation for ${\mathbf{f}}_{\text{r}}$ without loss of generality is:

$$ {\mathbf{x}}_{\text{pos}} {\mathbf{ = R}}^{\text{pos - 1}} {\mathbf{R}}^{\text{pat}} {\mathbf{x}}_{\text{plan}} {\mathbf{ - R}}^{\text{pos - 1}} {\mathbf{R}}^{\text{pat}} {\mathbf{c}}_{\text{plan}}^{\text{iso}} {\mathbf{ + R}}^{\text{pos - 1}} \left( {{\mathbf{t}}^{\text{pat}} {\mathbf{ - t}}^{\text{pos}} } \right){\mathbf{ + c}}_{\text{pos}}^{\text{iso}} $$

(5)

where, for easy interpretation, the isocentre (${\mathbf{c}}_{\text{plan}}^{\text{iso}}$ and ${\mathbf{c}}_{\text{pos}}^{\text{iso}}$, in plan- and positioner spaces, respectively) of the C-arm is assumed as rotation centre for both patient- and positioner orientations, described by ${\mathbf{R}}^{\text{pat}}$ (DOF = 3 for ${\varvec{\upalpha}}^{\text{pat}}$ in Euler angles) and ${\mathbf{R}}^{\text{pos}}$ (DOF = 2 for C-arm primary- and secondary angles ${\varvec{\upalpha}}^{{{\text{c}} - {\text{arm}}}}$), respectively. The vector $\Delta {\mathbf{t}} = {\mathbf{t}}^{\text{pat}} - {\mathbf{t}}^{\text{pos}}$ represents relative translation between patient and positioner and, as indicated by Eq. (5), can be reduced to DOF = 3. These 8 variables are not independent but also have constraints imposed by clinical practice.

For the applications of interest, the patient position is assumed to take one of three discrete values in which the ERCP is performed, corresponding to the prone, left lateral, or supine position. Based on the current parameterisation, each patient position is optimised separately using a quasi-Newton method for the two remaining variables ${\varvec{\upalpha}}^{{{\text{c}} - {\text{arm}}}}$, to minimise the estimated TRE.

The three patient positions approximately correspond to three different orientations for ${\varvec{\upalpha}}^{\text{pat}}$. $\Delta {\mathbf{t}}$ may be calibrated with respect to external landmarks, such as palpable points on the ribs or vertebra, or tracked markers fixed to the surgical bed. However, neither can be estimated accurately before a procedure. Rotating a patient to a given angle or repositioning accurately during a procedure may be clinically infeasible, so it is more practical to estimate the bounds of the uncertainties ${\varvec{\Sigma}}_{{{\varvec{\upalpha}}^{\text{pat}} }}$ and ${\varvec{\Sigma}}_{{\Delta {\mathbf{t}}}}$ associated with ${\varvec{\upalpha}}^{\text{pat}}$ and $\Delta {\mathbf{t}}$, respectively. Whilst it is noted that error estimates in patient positioning can be derived from observed registration errors, the published values (e.g. [9]), summarized in Table 1, were used in this study to reflect a plausible clinical scenario. The C-arm orientation ${\varvec{\upalpha}}^{{{\text{c}} - {\text{arm}}}}$, on the other hand, can be calibrated to a high degree of accuracy. Therefore, its error is assumed negligible relative to that associated with patient positioning. If this error becomes significant, for example, if an uncalibrated C-arm is used, including an additional error in C-arm orientation should be considered.

Table 1. Result summary from two sets of patient data, errors are summarised using RMSE

Unlike estimation of intraoperative TRE, which can be conditioned on the registration transformation parameters, planning C-arm orientation and patient position has to take into account (marginalise over) the uncertainty in patient positioning (see also in Fig. 1). Given ${\varvec{\widehat{\upalpha }}}^{\text{pat}}$, the uncertainty in planning can be represented by an error covariance ${\varvec{\Sigma}}_{{{\varvec{\widehat{\upalpha }}}^{{{\text{c}} - {\text{arm}}}} }}$ on optimised ${\varvec{\widehat{\upalpha}}}^{{{\text{c}} - {\text{arm}}}}$. Now the entire process to compute the registered target position with parameterisation in Eq. (5) becomes:

$$ {\mathbf{u}}_{{\mathbf{r}}} = {\mathbf{f}}_{\text{p}} \left( {{\mathbf{f}}_{\text{r}} \left( {{\mathbf{r}},{\varvec{\widehat{\upalpha}}}^{{{\text{c}} - {\text{arm}}}} ,{\varvec{\widehat{\upalpha}}}^{\text{pat}} ,\Delta {\mathbf{t}}} \right)} \right). $$

Using the same treatment for Eqs. (2) and (3), a composite covariance matrix can be computed as follows:

$$ \widehat{\sum }_{{{\varvec{\widehat{\upalpha}}}^{{{\text{c}} - {\text{arm}}}} ,{\varvec{\widehat{\upalpha}}}^{\text{pat}} ,\Delta {\mathbf{t}}}} = \left({{\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{*T} {\varvec{\Sigma}}_{{{\mathbf{u}}_{{\mathbf{r}}} ,{\varvec{\widehat{\upalpha}}}^{\text{pat}} ,\Delta {\mathbf{t}}}}^{- 1} {\mathbf{J}}_{{{\mathbf{f}}_{\text{p}} }}^{*} } \right)^{+} $$

(6)

As in Eq. (3), ${\varvec{\Sigma}}_{{{\mathbf{u}}_{{\mathbf{r}}},{\varvec{\widehat{\upalpha}}}^{\text{pat}},\Delta {\mathbf{t}}}}$ can be constructed by ${{\varvec{\widehat{\Sigma}}}}_{{{\mathbf{u}}_{{\mathbf{r}}} }}$ estimated from Eq. (4) and uncertainty in patient positioning ${\varvec{\Sigma}}_{{{\varvec{\widehat{\upalpha}}}^{\text{pat}}}}$ and ${\varvec{\Sigma}}_{{\Delta {\mathbf{t}}}}$. The uncertainty in planning C-arm orientation ${{\varvec{\widehat{\Sigma}}}}_{{{\varvec{\widehat{\upalpha}}}^{{{\text{c}} - {\text{arm}}}}}}$ is the $2 \times 2$ leading principal submatrix. The estimated uncertainty in C-arm orientation provides an estimate of how precisely the C-arm position can be planned to achieve the estimated TRE that is optimal at the time of planning. For example, a 95 % confidence interval (CI) would indicate that the true optimised plan will be within the estimated region 95 % of the time. This may be considered together with other practical restrictions, such as the orientation range and control precision.

4 Experiment and Results

MRCP and ERCP were acquired for two patients who underwent ERCP-guided interventions under local research ethical approval. Anatomical landmarks were manually defined by an interventional radiologist, a gastroenterologist and three medical imaging research fellows, on separate occasions. These included points on the ampulla, hilum, L1-, L2-, T12 vertebrae, pancreatic genu, hepatic duct bifurcation, cystic duct- and pancreatic duct connections with the common bile duct, previously implanted surgical devices (e.g. a lap chole clip), and pathological features (e.g. a stricture). See an example in Fig. 2. LLEs for these points, summarised in Table 1, were estimated from the variance in the multiple landmarks. In addition, five validation landmarks for each case were defined to represent locations of clinical interest, such as points on the most distal aspect of the common bile duct and on the branches of the left- and right hepatic ducts.

Fig. 2.

A snapshot of the graphic user interface of MRCP-ERCP registration software, developed as part of this research. Landmarks are plotted with their respective uncertainties using 2D ellipse or 3D ellipsoids, corresponding to 90 % confidence levels. Left - preoperative MRCP with 3D landmarks (blue), targets (yellow) and the segmented biliary tree shown in green and grey; middle - a digitally reconstructed radiograph generated from the MRCP image with the estimated target TREs in yellow; right - ERCP with 2D landmarks (blue) and two example targets (registered targets are shown in yellow, whereas validation targets are shown in red).

Monte-Carlo simulations were used to verify: (1) the TRE estimated by Eq. (4); and (2) the derived planning uncertainty given by Eq. (6), where Jacobian was estimated numerically. 10,000 simulations were performed sampling respective variables. As an example, Fig. 3, the overall agreement is excellent with 4.5 ± 3.6 % difference between the TRE computed analytically versus the result of numerical simulations, measured as the RMSE in ${\varvec{\Sigma}}_{{{\mathbf{u}}_{{\mathbf{r}}} }}$. The overall RMSE had a range of [3.2, 9.8] mm between different C-arm positions. The difference in ${\varvec{\Sigma}}_{{{\varvec{\widehat{\upalpha}}}^{{{\text{c}} - {\text{arm}}}}}}$ was 17.9 ± 9.7 % when the RMSE is smaller than 50°, which we consider as a planning range. As the planning error increased, Eq. (6) provided an increasingly poor approximation with up to ~500 % difference from simulation results. This is to be expected given that there are only 2 DOFs in this case.

Fig. 3.

Estimated TREs (RMSE in mm is indicated by the colour bar) for two example targets - a bifurcation at left hepatic duct (left plot) and a stricture at pancreatic duct (right plot) - computed using Monte-Carlo simulation (solid-line ellipse) versus analytical results (coloured ellipse), for different C-arm orientations (in degrees). Please see the text for the experiment details.

The measured TRE was computed for each of the target for ERCP images acquired at different, but sub-optimal C-arm angles (due to the retrospective analysis). The results, compared with the estimated TRE and planning error, are summarised in Table 1. Although the estimated TREs significantly under-estimated the observed values for both patients, possibly due to rigid assumption, a trend implying potential predictive ability was observed (correlation coefficient of 0.95). Significant differences in both estimated- and observed registration accuracy were found for Patient 1, for different C-arm angles (both p-values < 0.01), which is consistent with the estimated planning errors that produce mutually exclusive 90 % CIs. Patient 2 had a larger planning error (overlapping each other within respective 50 % CIs) for both C-arm orientations, predicting that significant changes in TRE are unlikely. This was confirmed by insignificant differences from both estimated- and observed TREs (p-values = 0.99 and 0.07).

5 Conclusion and Discussion

Three main contributions have been identified in the proposed planning-informed registration method: (a) a new error propagation approach is derived, incorporating uncertainties in 2D- and 3D landmark identification, to estimate a TRE for 2D-3D registration in ERCP-guided procedures; (b) a novel method for handling uncertainty in planning is introduced to assess a planning protocol in which C-arm orientation and patient position are optimised to achieve a minimum estimated TRE; and (c) presentation of preliminary results from real patient data that validate the derived error propagation methods and demonstrate possible clinical utility of the proposed methods.

The proposed error propagation method may be extended to non-rigid registration, in particular, to inform planning strategies to maximise registration accuracy. The assumption of a Gaussian distribution provides a reasonable and convenient approximation for the purpose of surgical planning, but the registration landmark and patient positioning error distributions may be non-Gaussian. In this case, alternative methods, such as unscented filtering, may be applicable. The values of LLEs and uncertainty in patient positioning are estimated using a relatively small sample size and from literature. Current results in Sect. 4 are based on retrospective image data which do not have optimised C-arm orientation. A larger prospective patient study will be able to further validate the proposed methods.