Manifold Mixing for Stacked Regularization

Abstract

In many real-world learning tasks, one has access to datasets consisting of multiple modalities, for example, various omics profiles of the patients coupled with medical records and other unstructured data sources. Often, the “core mechanism” (e.g. health or disease state) is reflected in all of these modalities and so this commonality can become more evident when the source domain (e.g. proteins) can accordingly transform the local geometry of the target (e.g. lipids). In this paper, we propose a novel algorithm that takes multiple data sources, constructs corresponding manifolds, and “mixes” information across them to find the common denominators in the observable outcomes. By leveraging manifold information from these different sources we obtain more robust and accurate results in comparison to standard methods. In the empirical evaluation on a clinical cohort related to ischaemia in patients with coronary artery disease, we demonstrate the applicability and efficacy of the proposed algorithm.

1 Introduction

Exponential increase in multi-modal data, stemming from different instruments and measurements presents both an opportunity and a challenge. With a larger sheer volume of information, there is potentially more we can learn for a given process, but coherently combining different data sources with the goal of improving analysis remains a challenging and underdeveloped task. In the medical field for instance, multiple omics data such as proteins or lipids encode somewhat related biological information. Therefore, one might expect that health or disease state is reflected in both of these modalities, despite their different format. Learning frameworks such as manifold alignment [5, 10] and domain adaptation [6, 8] may not be directly applicable as they try to find a common latent manifold and learn to transfer knowledge from a source to a target domain, respectively. Orthogonally to existing methods, we present a way of “mixing” information from multiple domains, without imposing hard similarity between them. The motivation is that for a given outcome, the “core mechanism” (e.g. health or disease state) is reflected in all of these modalities and so this commonality can become more evident when the source domain (e.g. proteins) can accordingly transform the local geometry of the target (e.g. lipids).

2 Approach

We use a stacked regularization setting [11] where each level-one model is trained using “mixed manifolds” of various data modalities. In the next subsections we briefly discuss classical stacked regularization, domain alignment, adaption, and finally propose our mixing algorithm. Regarding notation, we will use capital bold, bold and no formatting for matrices, vectors and scalars or functions, respectively (e.g. $\mathbf {\mathbf {X}}, \mathbf {x}, f$/W). We will also use calligraphic font to denote spaces (e.g. $\mathcal {X}$).

2.1 Stacking

Let $\mathbf {\mathbf {X}}$ be a dataset of N samples whose values are sampled from an input space $\mathcal {X}=\{\mathcal {X}^1,\, \mathcal {X}^2,\, ...,\,\mathcal {X}^M\}$ where $\mathcal {X}^1$ to $\mathcal {X}^M$ are subspaces corresponding to different “sources” or “views” $1\rightarrow M$ which we will refer to as “domains”. Denote by y the output sampled from an output space $\mathcal {Y}$. In a supervised setting, the goal is to compute $p\left( y|\mathbf {x}^{1},\,...,\,\mathbf {x}^{M}\right)$, where $\mathbf {x}^{i}$ are the coordinates of an instance from $\mathbf {\mathbf {X}}$ in the domain $\mathcal {X}^i$. In stacked regularization, or stacking, the input is passed to a first layer of $W_0$ predictors $g^0_1(\mathbf {x}),\,...,g^0_{W_0}(\mathbf {x})$, with:

$$\begin{aligned} g^0_i(\mathbf {x})=p\left( y|\mathbf {x}^{1},\,...\,\mathbf {x}^{M},\,\varvec{\theta }_{i}^0\right) {,} \end{aligned}$$

(1)

where $\varvec{\theta }_{i}^0$ are the hyperparameters of the ith model. For our task, we suggest to pass one data source per model: $g^0_i(\mathbf {x})=p\left( y|\mathbf {x}^{i},\,\varvec{\theta }_{i}^0\right)$, so that the width of the first layer $W_0$ is equal to the number of domains M. The output from this layer is then passed to one or more layers of $W_k$ models $g_{1}^k,\,...,g^k_{W_k}$ which blend the outputs of the previous ones:

$$\begin{aligned} g^k_i(\mathbf {x})=p\left( y|g^{k-1}_1(\cdot ),\,...,\,g^{k-1}_{W_k}(\cdot )),\,\varvec{\theta }_{i}^k\right) ,\,k\in [1, L]{,} \end{aligned}$$

(2)

where L is the total number of blending layers and $\varvec{\theta }_{i}^k$ the hyperparameters of ith model from the kth layer. The last blending layer is then passed to a final model f that produces the output $f(\mathbf {x})=p\left( y| g^{L}_1(\mathbf {x}),\,...,\,g^{L}_{W_L}(\mathbf {x}),\,\varvec{\theta }^{L+1}\right)$, where $\varvec{\theta }^{L+1}$ are the hyperparameters of f. You can visualize the stacked model general architecture in Fig. 1. From a frequentist point of view, the goal of stacking is then to find:

$$\begin{aligned} \underset{\varvec{\theta }}{arg min} \,\,\mathcal {L}(\mathbf {y}; f(\mathbf {\mathbf {X}}), \varvec{\theta }){,} \end{aligned}$$

(3)

where $\varvec{\theta }$ is the set of hyperparameter values from all of the stack models, $\mathbf {y}$ is the output for all of the data, and $\mathcal {L}$ is the loss function when using $f(\mathbf {x})$ to predict $\mathbf {y}$. For a fully Bayesian approach, one should compute the posterior probability of each model by integrating out the hyperparameter values:

$$\begin{aligned} \begin{aligned} p\left( g_i^k|Z\right) \propto p\left( Z|g_i^k\right) p\left( g_i^k\right) \propto \\ p\left( g_i^k\right) \int p\left( Z|\varvec{\theta }_i^k, g_i^k\right) p\left( \varvec{\theta }_i^k|g_i^k\right) d\varvec{\theta }_i^k{,} \end{aligned} \end{aligned}$$

(4)

where Z is the complete dataset $(\mathbf {X},\mathbf {y})$.

Fig. 1.

Our proposed stacked setting

Although this approach is attractive because it considers the uncertainty of the model, it also incurs high computational cost for large $\varvec{\theta }_i^k$.

Two important aspects are: (a) optimizing each model independently does not guarantee finding the global optimal stacked model and (b) there is an implicit assumption that each model $g_i^k$ can learn/handle data from different sources (possibly with different formats) effectively.

2.2 Stacking Optimization

Finding an optimal stacked model can be done by optimizing each sub-model individually or by jointly optimizing all the sub-models. Optimizing each model individually has an important complexity advantage because the number of possible $\varvec{\theta }$ combinations increases exponentially with the number of parameters: $k^{|\varvec{\theta }|}$, where k is the number of values considered for each parameter.

Lemma 1

For a given dataset $\mathbf {X}, \mathbf {y}$, stacked model f(x) and parameters $\varvec{\theta }$, the following relation is true: $\mathcal {L}\left( \mathbf {y}, f(x), \varvec{\theta }^{*} \right) \le \mathcal {L}\left( \mathbf {y}, f(x), \varvec{\theta }' \right)$, where

$\varvec{\theta }^{*} =\underset{\varvec{\theta }}{arg min}\,\,\mathcal {L}\left( \mathbf {y}, f(x), \varvec{\theta } \right)$, $\varvec{\theta }' = \varphi _{k=1}^L \left( \varphi _{i=0}^{W_k}\left( \; \underset{\varvec{\theta }^k_i}{arg min}\,\,\mathcal {L}\left( \mathbf {y}, g_i^k(x), \varvec{\theta }_i^k \right) \right) \right)$, and $\varphi _{j=1}^{L}\left( \underset{\varvec{\theta }_{j}}{arg min}\,f(\varvec{\theta _j})\right)$ is a sequential composition of minimizations with respect to index j: $\underset{\varvec{\theta }_{j=L}}{arg min}\left( \underset{\varvec{\theta }_{j=L-1}}{arg min}\left( ...\,\underset{\varvec{\theta }_{j=1}}{arg min}\left( f(\varvec{\theta _j}) \right) \right) \right)$.

Proof

Let $\mu$ be a measure on the measurable space $(\varTheta , \varvec{\theta })$. Since $\varvec{\theta }$ is a disjoint set, its measure is just:

$$\begin{aligned} \mu (\varvec{\theta }) = \prod _{k=0}^{L+1}\prod _{i=1}^{W_k}\mu (\varvec{\theta }_i^k) \end{aligned}$$

(5)

Denote by $\{\varvec{\theta }_i^{k}\}^*$ the set of values that satisfy $\underset{\varvec{\theta }^k_i}{arg min}\,\,\mathcal {L}\left( \mathbf {y}, g_i^k(x), \varvec{\theta }_i^k \right)$, and $\{\varvec{\theta }_i^k\}$ the set of values $\varvec{\theta }_i^k$ can take. Since $\{\varvec{\theta }_i^{k}\}^* \subset \{\varvec{\theta }_i^k\}$, then $\mu \left( \{\varvec{\theta }_i^{k}\}^*\right) \le \mu \left( \{\varvec{\theta }_i^k\}\right) ,\,\forall \; i,k$, and so:

$$\begin{aligned} \mu \left( \varvec{\theta }'\right) =\prod _{k=0}^{L+1}\prod _{i=1}^{W_k}\mu \left( \{\varvec{\theta }_i^{k}\}^*\right) \le \prod _{k=0}^{L+1}\prod _{i=1}^{W_k}\mu \left( \{\varvec{\theta }_i^{k}\}\right) \end{aligned}$$

(6)

$\mathcal {L}\left( \mathbf {y}, f(x), \varvec{\theta }^{*} \right)$ is thus optimizing over a larger domain than $\mathcal {L}\left( \mathbf {y}, f(x), \varvec{\theta }' \right)$ is, yielding $\mathcal {L}\left( \mathbf {y}, f(x), \varvec{\theta }^{*} \right) \le \mathcal {L}\left( \mathbf {y}, f(x), \varvec{\theta }' \right)$

There is a trade-off between complexity and performance when it comes to optimizing the model. If performance is the goal, then the next step is to decide what form is the optimization going to take. A grid-search would quickly become unfeasible for models with multiple hyperparameters, so an attractive solution is to instead use Bayesian optimization [1].

2.3 Domain Alignment

Note that at this point there is no information sharing between the first layer’s models. However, in many situations it may be desirable that some information is shared across these models since they are build using different modalities of the same sample set. The motivation is that even though the samples come from different distributions, the generating processes should be similar and thus they should lie in a similar low-dimensional manifold. This is the central problem of Manifold Alignment [7]. Our Manifold Mixing is based on similar motivation, with crucial difference - we consider that each domain has a contribution of its own, and therefore we will not enforce an exact match between the manifolds but merely a transformation of the local inter-sample geometry using all the domains, indirectly linking the stacked first layer models together.

2.4 Domain Adaptation

Given two domains $\mathcal {X}^s$ and $\mathcal {X}^t$, that are different but related, the goal of Domain Adaptation is that of learning to transfer knowledge acquired from the source $\mathcal {X}^s$ to the target $\mathcal {X}^t$. The most common setting is when there are many labeled examples in the source, but not in the target, and therefore one tries to learn an estimator h such that it minimizes the error on both the source and target distribution prediction [2]. In our setting, the source and target domains represent different modalities of the same sample. For clarity, we will use source and target domain definitions as well, and use the former to transform the latter.

2.5 Manifold Mixing

We would like to address the question: how to combine data from different domains with a similar relation to the output? Our approach consists in creating a map between each pair of domains $\mathcal {X}^{s}\rightarrow \mathcal {X}^{t}$, while deforming the local geometry of the two to become more similar. We drew inspiration from LLE [9] in that we will also use the neighbours of a point to predict its position. In our case, we will use the neighbours of this point in the other domains to predict its position in the original domain. Consider a set of points S and two mappings taking the points in S to two coordinate systems of domains $\mathcal {X}^t$ and $\mathcal {X}^s$: $\varphi : S \rightarrow \mathbb {R}^{|t|}$, $\psi : S \rightarrow \mathbb {R}^{|s|}$, and suppose the subsets $\mathbf {X}^t$, $\mathbf {X}^s$ of the dataset $\mathbf {X}$ are measured in these coordinate systems. Let us introduce an approximation $\mathbf {L}_{s}^{t}$ to the mapping $\varphi \circ \psi ^{-1}: \mathbb {R}^{|s|}\rightarrow \mathbb {R}^{|t|}$ from the coordinates of domain $\mathcal {X}^s$ to the coordinates of domain $\mathcal {X}^t$: $\underset{\mathbf {L}_{s}^{t}}{\min }\sum _{i=1}^{N}||\mathbf {x}_i^t - \mathbf {L}_{s}^{t}\mathbf {x}_i^{s}||^2$, with $\mathbf {x}_i^t, \mathbf {x}_i^{s}$ corresponding to the ith entry of $\mathbf {X}^t$ and $\mathbf {X}^s$, respectively. The optimal solution is then given by:

(7)

Fig. 2.

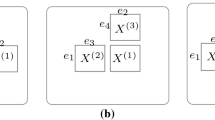
Target manifold being deformed by the source manifold using the manifold mixing method. The crosses are the neighbours of point $\mathbf {x}_i$ (point in red) in the target domain. These neighbours are mapped from the source to the target domain and then used to locate $\mathbf {x}_i$. This causes the target manifold to be locally deformed by the source manifold. (Color figure online)

Denote by $\mathbf {n}_i^t[j]$ the jth neighbour of instance $\mathbf {x}_i$ in the domain $\mathcal {X}^t$. Let the array of the points in $\mathcal {X}^s$ which are the neighbours of instance $\mathbf {x}_i^t$ in the domain $\mathcal {X}^t$ be: $\mathbf {N}_i^{s\leftarrow t} = \left[ \mathbf {x}_{\mathbf {n}_i^t[1]}^s, \mathbf {x}_{\mathbf {n}_i^t[2]}^s, \,\dots ,\mathbf {x}_{\mathbf {n}_i^t[k]}^s\right]$. Our goal is to ‘mix’ information from different manifolds. This is accomplished by projecting the neighbours of $\mathbf {x}_i^t$ from the source to the target domain and then finding the linear combination of the points that best reconstructs $\mathbf {x}_i^t$ in the original domain:

$$\begin{aligned} \underset{\mathbf {w}_{i}}{\min }\sum _{i}||\mathbf {x}_i^t - \tilde{\mathbf {x}}_i^{t\leftarrow s}||^2=\underset{\mathbf {w}_{i}}{\min }\sum _{i}||\mathbf {x}_i^t - L_{s}^{t}\mathbf {N}_i^{s\leftarrow t}\mathbf {w}_i||^2, \end{aligned}$$

(8)

where $\tilde{\mathbf {x}}_i^{t\leftarrow s}$ is the reconstruction of $\mathbf {x}_i^t$ using domain $\mathcal {X}^s$. We visualize how substituting $\mathbf {x}_i$ by $\tilde{\mathbf {x}}_i^{t\leftarrow s}$ might affect the target manifold in Fig. 2. After setting the derivative w.r.t. $\mathbf {w}_i$ to zero, the optimal solution corresponds to:

(9)

where $\mathbf {\tilde{N}}^{t\leftarrow s}_i=\mathbf {L}_{s}^{t}\mathbf {N}^{s\leftarrow t}$, the neighbors of $\mathbf {x}_i$ in $\mathcal {X}_t$ projected from their coordinates in $\mathcal {X}_s$ back to the coordinates in $\mathcal {X}_t$. We can now transform the original space $\mathcal {X}^t$ into the space reconstructed from the other domains $\tilde{\mathcal {X}}^t$ by computing for each instance the weighted mean of its reconstructions:

$$\begin{aligned} \tilde{\mathbf {x}}_i^t=\beta _t \mathbf {x}_i^t + \sum _{s\ne d}\beta _{s}\tilde{\mathbf {x}}_i^{t\leftarrow s}{,} \end{aligned}$$

(10)

where $\beta _j$ can be seen as the prior of domain $\mathcal {X}^j$’s relevance, and $\sum _{j}\beta _j = 1$. When evaluating a new point $\mathbf {x}_{new}$, first the nearest neighbours from the training set are found, and then the reconstruction is given by $\mathbf {\tilde{N}}^{s\leftarrow t }_i \mathbf {w}_{new}$. The complexity of the algorithm is bounded by the matrix inversion of the coordinate mapping in Eq. 7, and therefore the algorithm complexity is $\mathcal {O}(d^3)$, where d is the maximum number of features among all the domains.

3 Experimental Section

3.1 Methods

To test our method we used a recent clinical cohort [3] containing data on patients with cardiovascular disease. There are 440 subjects in the dataset of which 56 suffered from an early cardiovascular event. For each patient, 359 protein levels and 9 clinical parameters are measured. We evaluate performance our method (stacked regularization with manifold mixing) for predicting a cardiovascular event. We compare proposed approach to that of using a standard stacked model with joint Bayesian optimization of the hyper-parameters, as well as with using random forest on the merged/ feature concatenated datasets (protein levels and clinical parameters). For both our method and the standard stacking, the architecture consisted of two larger random forest models in the first layer and a smaller one in the output.

3.2 Data Selection and Preprocessing

We perform random shuffles with $90\%$ train size and even class distribution in the train/test set. We use remaining $10\%$ to test the model. Since the dataset is unbalanced (much larger number of negative than positive subjects), we took a random sample from the negative class of size equal to the total number of positive class subjects, prior to the split at each shuffle. The protein were measured using a technology that uses standard panels for different proteins, meaning some of the proteins might have no relation to the outcome at all. For this reason, for each run we pre-selected 50 proteins using Univariate Feature Selection on the training set. Then, we normalized the train and test data independently, and measured the average ROC for each of the methods. We perform 5-fold cross validation for optimal hyper-parameter estimation on the train set for the random forests, and bayesian optimization for the stacked models. Once that is accomplished, we retrain the model with the optimal parameters on the complete training set and test on the remaining $10\%$. We repeat the this procedure multiple times and report the average ROC-AUC as well as the standard deviation. Described strategy is frequently referred to as stability selection procedure [4] The proteins were measured using OLINK technology that records expression levels of proteins via targeted and customised analysis [3].

3.3 Results

The results are presented in Fig. 3. Proposed approach (MM stacked) outperformed both the regular stacked model and the random forests (RF) using the merged data. Both stacked regularized techniques outperformed standard RF.

Fig. 3.

Average AUC for the three methods compared. The highest performance is that of the Manifold Mixing stacked model (MM), and both stacked models outperformed using Random Forests (RF) on the merged data

4 Conclusions and Future Work

In this paper we propose the manifold mixing framework to improve the analysis of multi-modal data stemming from different sources. In our preliminary experiments, the obtained results support efficacy of our method. We outperform both standard stacked regularization and the model built on feature concatenated data. In the near future, we plan on performing further tests with larger number of shuffles, and testing on different datasets and heterogeneous domains. One pitfall of the current algorithm is the linearity of the map between manifolds which might fail in highly curved regions. A possible solution is to kernelize the method using graph kernels. Another interesting direction is to subdivide the manifold into multiple subregions based on the local curvature and create a mapping per subregion.