Keywords

1 Introduction

Alzheimer’s disease (AD) is a complex chronic progressive neurodegenerative disease that gradually affects human memory, judgment, and behavior. As an important intermediate stage between normal aging and AD, MCI possesses an increased risk of transiting to AD. That being the case, how to recognize the MCI samples with high potential of switching to AD prior to dementia becomes an essential problem in Alzheimer’s prophylaxis and early treatment.

Neuroimaging provides an effective tool to characterize the structure and functionality of nervous system, thus has greatly contributed to Alzheimer’s study [22]. Extensive work has been proposed to predict MCI conversion using neuroimaging data [6, 15]. Previous methods usually formulate MCI conversion prediction as a binary classification (distinguishing MCI converters from non-converters) [15] or multi-class classification problem (when considering other classes such as AD or health control (HC)) [6], where the methods take the neuroimaging data at baseline time as the input and classify if the MCI samples will convert to AD in years.

Despite the prosperity and progress achieved in MCI conversion prediction, there are still several problems existing in previous methods. (1) Although we expect the model to be capable of forecasting the MCI conversion years before the change of disease status, the training process should not be limited to just baseline data. In the longitudinal study of AD, usually the data at several time points along the disease progression is available, such as baseline, month 6, month 12, etc. However, previous methods only consider the baseline data in the training process, thus ignore the temporal correlation structure among other time points.

(2) The labeling process for Alzheimer’s is time-consuming and expensive, so the MCI conversion prediction suffers greatly from limited training data.

To deal with these problems, we propose a novel model for MCI conversion prediction. Firstly, we study the temporal correlation structure among the longitudinal data in Alzheimer’s progression. Since AD is a chronically progressive disorder and the neuroimaging features are correlated [11], it can be helpful to analyze the temporal correlation between neuroimaging data in the disease progression as in other nervous system diseases [3]. We construct a regression model to discover such temporal correlation structure between adjacent time points. Our model incorporates the data at all time points along the disease progression and uncovers the variation trend that benefits MCI conversion prediction.

Secondly, we construct a classification model to predict the disease status at each time point. Different from previous classification models that use the baseline data to forecast the progression trend in two or three years, our classification model focuses on adjacent time points. Compared with previous models that require a highly distinguishable conversion pattern appears several years before dementia, our model predicts the progression trend for consecutive time points, thus is more accurate and reliable.

Thirdly, we construct a generative model based on generative adversarial network (GAN) to produce more auxiliary data to improve the training of regression and classification model. GAN model is proposed in [5], which uses the adversarial mechanism to learn the inherent data distribution and generate realistic data. We use the generative model to learn the joint distribution of neuroimaging data at consecutive time points, such that more reliable training data can be obtained to improve the prediction of MCI conversion.

2 Temporal Correlation Structure Learning Model

2.1 Problem Definition

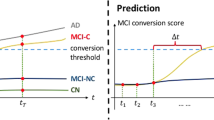
In MCI conversion prediction, for a certain sample and a time point t, we use \(\mathbf{x}_t \in \mathbb {R}^{p}\) to denote the neuroimaging data at time t while \(\mathbf{x}_{t+1} \in \mathbb {R}^{p}\) for the next time point, where p is the number of imaging markers. \(\mathbf{y}_t\in \mathbb {R}\) is the label showing the disease status at time t and \(t+1\). Here we define three different classes for \(\mathbf{y}_t\): \(\mathbf{y}_t=1\) means the sample is AD at both time t and \(t+1\); \(\mathbf{y}_t=2\) shows MCI at time t while AD at time \(t+1\); while \(\mathbf{y}_t=3\) indicates that the sample is MCI at both time t and \(t+1\). In the prediction, given the baseline data of an MCI sample, the goal is to predict whether the MCI sample will finally convert to AD or not.

2.2 Revisit GAN Model

GAN model is proposed in [5], which plays an adversarial game between the generator G and discriminator D. The generator G takes a random variable \(\mathbf{z}\) as the input and outputs the generated data to approximates the inherent data distribution. The discriminator D is proposed to distinguish the data \(\mathbf{x}\) from the real distribution and the data produced from the generator. Whereas the generator G is optimized to generate data as realistic as possible to fool the discriminator. The objective function of the GAN model has the following form.

$$\begin{aligned} \min _G \max _D~\mathbb {E}_{\mathbf{x}\sim { p}(\mathbf{x})} \big [\log (D(\mathbf{x}))\big ] + \mathbb {E}_{\mathbf{z}\sim { p}(\mathbf{z})} \big [\log (1-D(G(\mathbf{z}))\big ], \end{aligned}$$

where \(p(\mathbf{z})\) denotes the distribution of the random variable and \(p(\mathbf{x})\) represents the distribution of real data. The min-max game played between G and D improves the learning of both the generator and discriminator, such that the model can learn the inherent data distribution and generate realistic data.

Fig. 1.
figure 1

Illustration of our Temporal-GAN model. \(\mathbf{x}_t\) and \(\mathbf{x}_{t+1}\) are the neuroimaging data at two adjacent time points and \(\mathbf{y}_t\) is the label (\(\mathbf{y}_t=1\) if both \(\mathbf{x}_t\) and \(\mathbf{x}_{t+1}\) are at AD status; \(\mathbf{y}_t=2\) if \(\mathbf{x}_t\) is MCI while \(\mathbf{x}_{t+1}\) is AD; \(\mathbf{y}_t=3\) if both \(\mathbf{x}_t\) and \(\mathbf{x}_{t+1}\) are MCI.). The regression network R predicts \(\mathbf{x}_{t+1}\) from \(\mathbf{x}_t\) so as to uncover the temporal correlation between adjacent time points. The classification network C predicts the label \(\mathbf{y}_t\) from \(\mathbf{x}_t\). We also construct a generative model with generator G and discriminator D to approximate the joint distribution underlying data pair \(([\mathbf{x}_t,\mathbf{x}_{t+1}],\mathbf{y}_t)\) to generate more reliable data for training R and C. In the prediction process, the neuroimaging data \(\mathbf{x}_0\) at baseline time for MCI samples is given, and we use R and C to predict whether the MCI sample will convert to AD at time T.

Full size image

2.3 Illustration of Our Model

Inspired by [2], we propose to approximate the joint distribution of neuroimaging data at consecutive time points and data label \(([\mathbf{x}_t,\mathbf{x}_{t+1}],\mathbf{y}_{t})\sim p(\mathbf{x},\mathbf{y})\) by considering the following:

$$\begin{aligned} \begin{aligned} \min _{G_t, G_{t+1}} \max _D~&\mathbb {E}_{([\mathbf{x}_t,\mathbf{x}_{t+1}],\mathbf{y}_{t})\sim p(\mathbf{x},\mathbf{y})}[\log (D([\mathbf{x}_t,\mathbf{x}_{t+1}],\mathbf{y}_{t}))]\\ +~&\mathbb {E}_{\mathbf{z}\sim { p}(\mathbf{z}),\mathbf{y}\sim { p}(\mathbf{y})}[\log (1-D([G_t(\mathbf{z},\mathbf{y}), G_{t+1}(\mathbf{z},\mathbf{y})], \mathbf{y}))], \end{aligned} \end{aligned}$$

where the generators take a random variable \(\mathbf{z}\) and a pseudo label \(\mathbf{y}\) as the input and output a data pair \(([G_t(\mathbf{z},\mathbf{y}), G_{t+1}(\mathbf{z},\mathbf{y})], \mathbf{y})\) that is as realistic as possible. Still, the discriminator is optimized to distinguish real from fake data. The construction of such generative model approximates the inherent joint distribution of neuroimaging data at adjacent time points and label, which generates more reliable samples for the training process.

To uncover the temporal correlation structure among the neuroimaging data between consecutive time points, we construct a regression network R to predict \(\mathbf{x}_{t+1}\) from \(\mathbf{x}_t\), such that progression trend among neuroimaging data along the disease progression can be learned. The network R takes data from both real distribution and the generators as the input and optimize the following:

$$\begin{aligned} \begin{aligned} \min _R~&\mathbb {E}_{([\mathbf{x}_t,\mathbf{x}_{t+1}],\mathbf{y}_{t})\sim p(\mathbf{x},\mathbf{y})}[\Vert \mathbf{x}_{t+1}-R(\mathbf{x}_t)\Vert _1]\\ +~&\lambda _{reg}\mathbb {E}_{\mathbf{z}\sim { p}(\mathbf{z}),\mathbf{y}\sim { p}(\mathbf{y})}[\Vert G_{t+1}(\mathbf{z},\mathbf{y})-R(G_{t}(\mathbf{z},\mathbf{y}))\Vert _1], \end{aligned} \end{aligned}$$
(1)

where the hyper-parameter \(\lambda _{reg}\) balances the importance of real and generated data. We consider \(\ell _1\)-norm loss to make the model R more robust to outliers.

In addition, we construct a classification structure C to predict the label \(\mathbf{y}_t\) given data \(\mathbf{x}_t\). The optimization of C is based on the following:

$$\begin{aligned} \begin{aligned} \min _C~&-\mathbb {E}_{([\mathbf{x}_t,\mathbf{x}_{t+1}],\mathbf{y}_{t})\sim p(\mathbf{x},\mathbf{y})}[\mathbf{y}_t \log (C(\mathbf{x}_t))]\\ -~&\lambda _{cly}\mathbb {E}_{\mathbf{z}\sim { p}(\mathbf{z}),\mathbf{y}\sim { p}(\mathbf{y})}[\mathbf{y}\log (C(G_t(\mathbf{z})))], \end{aligned} \end{aligned}$$
(2)

where \(\lambda _{cly}\) is a hyper-parameter to balance the role of real and generated data.

Given a set of real data \(\{([\mathbf{x}_t^i,\mathbf{x}_{t+1}^i],\mathbf{y}_t^i)\}_{i=1}^n\), the above three loss terms can be approximated by the following empirical loss:

$$\begin{aligned}&{\mathcal {L}}_{adv} = \frac{1}{n} \sum \limits _{i=1}^n \log (D([\mathbf{x}_t^i,\mathbf{x}_{t+1}^i],\mathbf{y}_t^i)) + \sum \limits _{j=1}^{n_z} \log (D([G_t(\mathbf{z}^j,\mathbf{y}^j),G_{t+1}(\mathbf{z}^j,\mathbf{y}^j)],\mathbf{y}^j)),\\&{\mathcal {L}}_{reg} = \frac{1}{n} \sum \limits _{i=1}^n \Vert \mathbf{x}_{t+1}^i-R(\mathbf{x}_t^i)\Vert _1 + \lambda _{reg}\sum \limits _{j=1}^{n_z} \Vert G_{t+1}(\mathbf{z}^j,\mathbf{y}^j)-R(G_{t}(\mathbf{z}^j,\mathbf{y}^j))\Vert _1,\\&{\mathcal {L}}_{cly} = -\frac{1}{n} \sum \limits _{i=1}^n {{\mathbf{y}}_t^i \log (C({\mathbf{x}}_t^i))} - \lambda _{cly}\sum \limits _{j=1}^{n_z} {{\mathbf{y}}^j \log (C(G_t({\mathbf{z}}^j,{\mathbf{y}}^j)))}. \end{aligned}$$

For a clear illustration, we plot a figure in Fig. 1 to show the structure of our Temporal-GAN model (temporal correlation structure learning for MCI conversion prediction with GAN). The implement details of the networks can be found in the experimental setting section. The optimization of our model is based on a variant of mini-batch stochastic gradient descent method.

3 Experimental Results

3.1 Experimental Setting

To evaluate our Temporal-GAN model, we compare with the following methods: SVM-Linear (support vector machine with linear kernel), which has been widely applied in MCI conversion prediction [6, 15]; SVM-RBF (SVM with RBF kernel), as employed in [10, 21]; and SVM-Polynomial (SVM with polynomial kernel) as used in [10]. Also, to validate the improvement by learning the temporal correlation structure, we compare with the Neural Network with exactly the same structure in our classification network (network C in Fig. 1) that only uses baseline data. Besides, we compare with the case where we do not use the GAN model to generate more auxiliary samples, i.e., only using network C and R in Fig. 1, which we call Temporal-Deep.

The classification accuracy is used as the evaluation metric. We divide the data into three sets: training data for training the models, validation data for tuning hyper-parameters, and testing data for reporting the results. We tune the hyper-parameter C of SVM-linear, SVM-RBF and SVM-Polynomial methods in the range of \(\{10^{-3},~10^{-2},~\dots ,~10^3\}\). We compare the methods when using different portion of testing samples and report the average performance in five repetitions of random data division.

In our Temporal-GAN model, we use the fully connected neural network structure for all the networks G, D, R and C, where each hidden layer contains 100 hidden units. The implementation detail is as follows: the number of hidden layers in structure G, D, R and C is 3, 1, 3, 2 respectively. We use leaky rectified linear unit (LReLU) [12] with leakiness ratio 0.2 as the activation function of all layers except the last layer and consider weight normalization [14] for layer normalization. Also, we utilize the dropout mechanism in the regression structure R with the dropout rate of 0.1. The weight parameters of all layers are initialized using the Xavier approach [4]. We use the ADAM algorithm [9] to update the weight parameters with the hyper-parameters of ADAM algorithm set as default. Both values of \(\lambda _{reg}\) in Eq. (1) and \(\lambda _{cly}\) in Eq. (2) are set as 0.01.

3.2 Data Description

All data were downloaded from the ADNI database (adni.loni.usc.edu). Each MRI T1-weighted image was first anterior commissure (AC) posterior commissure (PC) corrected using MIPAV2, intensity inhomogeneity corrected using the N3 algorithm [17], skull stripped [20] with manual editing, and cerebellum-removed [19]. We then used FAST [23] in the FSL package3 to segment the image into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF), and used HAMMER [16] to register the images to a common space. GM volumes obtained from 93 ROIs defined in [8], normalized by the total intracranial volume, were extracted as features. Out of the 93 ROIs, 24 disease-related ROIs were involved in the MCI prediction [18]. This experiment includes data from six different time points: baseline (BL), month 6 (M6), month 12 (M12), month 18 (M18), month 24 (M24) and month 36 (M36). All 216 samples with no missing MRI features at BL and M36 time are used by all the comparing methods, where there are 101 MCI converters (MCI at BL time while AD at M36) as well as 115 non-converters (MCI at both BL and M36). Since our Temporal-GAN model can use data at time points other than BL and M36, we include a total of 1419 data pairs with no missing neuroimaging measurement for training the classification, regression and generative model in our Temporal-GAN model. All neuroimaging features in the data are normalized to zero mean and unit variance.

3.3 MCI Conversion Prediction

We summarize the MCI conversion classification results in Table 1. The goal of the experiment is to accurately distinguish converter subjects from non-converters among the MCI samples at baseline time. From the comparison we notice that Temporal-GAN outperforms all other methods under all settings, which confirms the effectiveness of our model. Compared with SVM-Linear, SVM-RBF, SVM-Polynomial and Neural Network, the Temporal-GAN and Temporal-Deep model illustrates apparent superiority, which validates that the temporal correlation structure learned in our model substantially improves the prediction of MCI conversion. The training process of our model takes advantage of all the available data along the progression of the disease, which provides more beneficial information for the prediction of MCI conversion. By comparing Temporal-GAN and Temporal-Deep, we can notice that Temporal-GAN always performs better than Temporal-Deep, which indicates that the generative structure in Temporal-GAN could provide reliable auxiliary samples to strengthen the training of regression R and classification C model, thus improves the prediction of MCI conversion.

Table 1. MCI conversion prediction with different portion of testing data.
Full size table
Fig. 2.
figure 2

Visualization figure showing the feature weights from our Temporal-GAN model. The upper figure shows features on the left hemisphere while the lower corresponds to the right hemisphere.

Full size image

3.4 Visualization of the Imaging Markers

We use feature weight visualization in Fig. 2 to validate if our Temporal-GAN can detect disease-related features when using all 93 ROIs in the MCI conversion prediction. We adopt the Layer-wise Relevance Propagation (LRP) [1] method to calculate the importance of neuroimaging features in the testing data. We can notice that our Temporal-GAN model selects several important features from all 93 ROIs. For example, our method identifies fornix as a significant feature in distinguishing MCI non-converters. The fornix is an integral white matter bundle that locates inside the medial diencephalon. [13] reveals the vital role of white matter in Alzheimer’s, such that the degradation of fornix indicates essential predictive power in MCI conversion. Moreover, cingulate region has been found by our model to be related with MCI converters. Previous study [7] finds significantly decreased Regional cerebral blood flow (rCBF) measurement in the left posterior cingulate cortex in MCI converters, which serves as an important signal in forecasting the MCI conversion. The replication of these findings proves the validity of our model.

4 Conclusion

In this paper, we proposed a novel Temporal-GAN model for MCI conversion prediction. Our model considered the data at all time points along the disease progression and uncovered the temporal correlation structure among the neuroimaging data at adjacent time points. We also constructed a generative model to produce more reliable data to strengthen the training process. Our model illustrated superiority in the experiments on the ADNI data.