Widespread chaos in rotation of the secondary asteroid in a binary system

Abstract

The chaotic behavior of the secondary asteroid in a system of binary asteroids due to the asphericity and orbital eccentricity is investigated analytically and numerically. The binary asteroids are modeled with a sphere–ellipsoid model, in which the secondary asteroid is ellipsoid. The first-order resonance is studied for different values of asphericity and eccentricity of the secondary asteroid. The results of the Chirikov method are verified by Poincare section which show good agreement between analytical and numerical methods. It is also shown that asphericity and eccentricity affect the size of resonance regions such that beyond the threshold value, the resonance overlapping occurs and widespread chaos is visible.

Appendices

Appendix 1

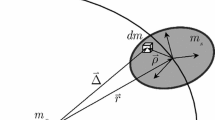
In this appendix, the potential energy for an ellipsoidal rigid body in gravitational field of point-mass body is derived. It is assumed that the ellipsoidal rigid body of the mass $m_s$ is subjected to the gravitational attraction of a point-mass or homogenous spherical body with the mass $m_p$. The distance between the two bodies is supposed to be large in comparison with the size of the ellipsoid body and also center of mass of the ellipsoid moves on a Keplerian orbit (see Fig. 9). The potential takes the form:

(27)

where $G$ is the universal gravitational constant and which is instantaneous orbital radius vector and is the position vector of $dm$ with respect to the center of mass of the ellipsoid.

Fig. 9

Sphere–ellipsoid configuration

The magnitude of can be expressed as

(28)

By using these representation

(29)

the inverse of $\varDelta$ is expanded by means of Legendre polynomials, $P_l$ as followed

$$\begin{aligned} \frac{1}{\varDelta }=\frac{1}{r\sqrt{1+\alpha ^{2}-2\alpha q}}=\frac{1}{r}\sum _{l=0}^\infty {\left( {-\alpha } \right) ^{l}P_l \left[ q \right] } \end{aligned}$$

(30)

The first four Legendre polynomials are

$$\begin{aligned} P_0 \left[ q \right]= & {} 1 \nonumber \\ P_1 \left[ q \right]= & {} q \nonumber \\ P_2 \left[ q \right]= & {} \frac{1}{2}\left( {3q^{2}-1} \right) \nonumber \\ P_3 \left[ q \right]= & {} \frac{1}{2}\left( {5q^{3}-3q} \right) \end{aligned}$$

(31)

which are utilized to derive approximate potential energy up to the third order, i.e.,

$$\begin{aligned} V\simeq V_0 +V_1 +V_2 +V_3 =\frac{\mathrm{Gm}_p }{r}\int \limits _{m_{s}} {\sum _{l=0}^3 {\left( {-\alpha } \right) ^{l}P_l \left[ q \right] } dm} \end{aligned}$$

(32)

The first term is

$$\begin{aligned} V_0 =-\frac{\mathrm{Gm}_p }{r}\int \limits _{m_{s}} {dm} =-\frac{\mathrm{Gm}_p m_s }{r} \end{aligned}$$

(33)

This is well-known Newton’s law of universal gravitation.

Forasmuch as the origin coincides with the center of mass, as said before, the second term is:

(34)

It follows that $V_2$ is expressed as:

(35)

By using these useful expressions

(36)

where $E$ is the unit matrix and $I$ is the moment of inertia tensor, the $V_2$ is followed as

(37)

By introducing unit vector

(38)

and considering that the moment of inertia is calculated in the body coordinate

$$\begin{aligned} \left[ I \right] ^\mathrm{ref}=T_B^\mathrm{ref} \left[ I \right] ^{B}T_\mathrm{ref}^B \end{aligned}$$

(39)

which $T_B^\mathrm{ref}$ and $T_\mathrm{ref}^B$ are transformation matrixes, transforming a vector from the body frame to the reference frame and vice versa, respectively, the final expression for $V_2$ is

$$\begin{aligned} V_2 =\frac{\mathrm{Gm}_p }{2r^{3}}\left\{ {3\hat{{r}}^{T}T_B^\mathrm{ref} \left[ I \right] ^{B}T_\mathrm{ref}^B \hat{{r}}-\hbox {Tr}\left[ I \right] } \right\} \end{aligned}$$

(40)

There are some integrals of the form $\int {x^{p}y^{q}z^{r}\,dm}$ in evaluating $V_3$. This integral for an ellipsoid which has three symmetry planes, is zero whenever one of $p, q, r$ is odd. According to fourth term of Legendre polynomial, $P_3$ contains only odd powers. Therefore, $V_3$ vanishes.

Thus the potential energy up to the third order is

$$\begin{aligned}&V\simeq V_0 +V_1 +V_2 +V_3 =-\frac{\mathrm{Gm}_p m_s }{r}\nonumber \\&\quad +\frac{\mathrm{Gm}_p }{2r^{3}}\left\{ {3\hat{{r}}^{T}\,T_B^\mathrm{ref} \left[ I \right] ^{B}T_\mathrm{ref}^B \hat{{r}}-\hbox {Tr}\left[ I \right] } \right\} \end{aligned}$$

(41)

Since in this paper only the rotational motion of ellipsoid rigid body is considered, the term of potential energy which contributes on the rotational motion is

$$\begin{aligned} V_\mathrm{rot} =\frac{\mathrm{Gm}_p }{2r^{3}}\left\{ {3\hat{{r}}^{T}\,T_B^\mathrm{ref} \left[ I \right] ^{B}T_\mathrm{ref}^B \hat{{r}}} \right\} \end{aligned}$$

(42)

Appendix 2

In this appendix, the Eq. (9) is derived in details. Consider the second term of the Hamiltonian

$$\begin{aligned} -\frac{\varepsilon ^{2}n^{2}I_3 }{4}\left( {\frac{a}{r}} \right) ^{3}\cos \left( {2\theta -2\!f} \right) \end{aligned}$$

(43)

The last part of this term can be written as

$$\begin{aligned}&\left( {\frac{a}{r}} \right) ^{3}\cos \left( {2\theta -2\!f} \right) \nonumber \\&\quad =\left( {\frac{a}{r}} \right) ^{3}\left( {\cos 2\theta \cos 2\!f+\sin 2\theta \sin 2\!f} \right) \end{aligned}$$

(44)

Also the $\cos 2\!f$ and $\sin 2\!f$ can be written in terms of sin and cos of the $f$:

$$\begin{aligned} \cos 2\!f= & {} 2\left( {\cos f} \right) ^{2}-1 \nonumber \\ \sin 2\!f= & {} 2\cos f\sin f \end{aligned}$$

(45)

Using the series function based on the Bessel functions of the first kind, the following relations are used and substituted in the above equation :

$$\begin{aligned} \left( {\frac{a}{r}} \right) ^{3}= & {} 1+3e\cos M+\frac{3}{2}e^{2}\left( {1+3\cos 2M} \right) +O\left( {e^{3}} \right) \nonumber \\ \sin f= & {} \sin M+e\sin 2M+e^{2}\left( {\frac{9}{8}\sin 3M-\frac{7}{8}\sin M} \right) \nonumber \\&+\,O\left( {e^{3}} \right) \nonumber \\ \cos f= & {} \cos M+e\left( {\cos 2M-1} \right) \nonumber \\&+\frac{9}{8}e^{2}\left( {\cos 3M-\cos M} \right) +O\left( {e^{3}} \right) \end{aligned}$$

(46)

Then

$$\begin{aligned}&\left( {\frac{a}{r}} \right) ^{3}\left( {\cos 2\theta \left( {2\left( {\cos f} \right) ^{2}-1} \right) +\sin 2\theta \left( {2\cos f\sin f} \right) } \right) \nonumber \\&\quad =\left[ {1+3e\cos M+\frac{3}{2}e^{2}\left( {1+3\cos 2M} \right) } \right] \nonumber \\&\quad \quad \times \Bigg \{ \cos 2\theta \Bigg [ 2\Bigg (\! \cos M+e\left( {\cos 2M-1} \right) \nonumber \\&\quad \quad +\frac{9}{8}e^{2}\left( {\cos 3M-\cos M} \right) \Bigg )^{2}-1 \Bigg ] \nonumber \\&\quad \quad +\sin 2\theta \Bigg [ 2\Bigg (\! \cos M+e\left( {\cos 2M-1} \right) \nonumber \\&\qquad +\frac{9}{8}e^{2}\left( {\cos 3M-\cos M} \right) \Bigg ) \nonumber \\&\quad \quad \left. {\left. {\times \left( {\sin M\!+e\sin 2M\!+e^{2}\left( {\frac{9}{8}\sin 3M\!-\frac{7}{8}\sin M} \!\right) } \!\right) } \!\right] } \!\right\} \nonumber \\ \end{aligned}$$

(47)

By simplifying above equation by elementary arithmetic and combining the terms and collecting all the coefficients with the same rational power of eccentricity up to third order of eccentricity, yields:

$$\begin{aligned} H= & {} \frac{p_\theta ^2 }{2I_3 }-\frac{\varepsilon ^{2}n^{2}I_3 }{4}\left\{ \cos \left( {2\theta -2M} \right) \right. \nonumber \\&\left. +\frac{e}{2}\left[ {-\cos \left( {2\theta -M} \right) +7\cos \left( {2\theta -3M} \right) } \right] \right. \nonumber \\&\left. {+\frac{e^{2}}{2}\left[ {-5\cos \left( {2\theta -2M} \right) +17\cos \left( {2\theta -4M} \right) } \right] } \right\} \nonumber \\&+O\left( {e^{3}} \right) \end{aligned}$$

(48)

All of the above manipulations can be done using every computer algebra software such as Maple${\copyright }$ and Mathematica${\copyright }$.