Pair correlation function of charge-stabilized colloidal systems under sheared conditions

Abstract

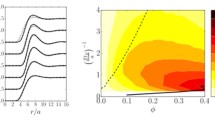
The pair correlation function of charge stabilized colloidal particles under strongly sheared conditions is studied using the analytical intermediate asymptotics method recently developed in Banetta and Zaccone (Phys. Rev. E 99, 052606 (2019) to solve the steady-state Smoluchowski equation for medium to high values of the Péclet number; the analytical theory works for dilute conditions. A rich physical behaviour is unveiled for the pair correlation function of colloids interacting via the repulsive Yukawa (or Debye-Hückel) potential, in both the extensional and compressional sectors of the solid angle. In the compression sector, a peak near contact is due to the advecting action of the flow and decreases upon increasing the coupling strength parameter Γ of the Yukawa potential. Upon increasing the screening (Debye) length κ^− 1, a secondary peak shows up, at a larger separation distance, slightly less than the Debye length. While this secondary peak grows, the primary peak near contact decreases. The secondary peak is attributed to the competition between the advecting (attractive-like) action of the flow in the compressions sector, and the repulsion due to the electrostatics. In the extensional sectors, a depletion layer (where the pair-correlation function is identically zero) near contact is predicted, the width of which increases upon increasing either Γ or κ^− 1.

Appendices

Appendix A: Mathematical formalism

Let’s focus or attention on the Brownian contribution to Eq. 16:

$$ \begin{array}{@{}rcl@{}} \tilde{\nabla} \cdot \left( \underline{\tilde{\textbf{D}}}^{\text{Br}} \cdot \tilde{\nabla} g(\tilde{\textbf{r}}) \right) - \tilde{\nabla} \cdot \left[ \left( \underline{\tilde{\textbf{D}}}^{\text{Br}} \cdot \tilde{\textbf{K}}^{\text{int}} \right) g(\tilde{\textbf{r}}) \right] \\ = \tilde{\nabla} \cdot \left( \underline{\tilde{\textbf{D}}}^{\text{Br}} \cdot \tilde{\nabla} g(\tilde{\textbf{r}}) \right) - \tilde{\nabla} \cdot \left( \underline{\tilde{\textbf{D}}}^{\text{Br}} \cdot \tilde{\textbf{K}}^{\text{int}} \right) g(\tilde{\textbf{r}})\\ -\left( \underline{\tilde{\textbf{D}}}^{\text{Br}} \cdot \tilde{\textbf{K}}^{\text{int}} \right) \cdot \tilde{\nabla} g(\tilde{\textbf{r}}) \end{array} $$

(36)

Expressing all the components and the divergence operator we obtain, respectively

$$ \begin{array}{@{}rcl@{}} &&\tilde{\nabla} \cdot \left[\begin{array}{lll} G(r) \frac{\partial g(\tilde{\textbf{r}})}{\partial \tilde{r}} \\ \\ \frac{H(r)}{\tilde{r}} \frac{\partial g(\tilde{\textbf{r}})}{\partial \theta} \\ \\ \frac{H(\tilde{r})}{\tilde{r} \sin{\theta}} \frac{\partial g(\tilde{\textbf{r}})}{\partial \phi} \end{array}\right] - \tilde{\nabla} \cdot \left[\begin{array}{lll} - G(\tilde{r}) \frac{d \tilde{U}}{d \tilde{r}} \\ \\ 0 \\ \\ 0 \end{array}\right] g(\tilde{\textbf{r}}) +\\ &&- \left[\begin{array}{lll} - G(\tilde{r}) \frac{d \tilde{U}}{d \tilde{r}} \\ \\ 0 \\ \\ 0 \end{array}\right] \cdot \left[\begin{array}{lll} \frac{\partial g(\textbf{r})}{\partial \tilde{r}} \\ \\ \frac{1}{\tilde{r}}\frac{\partial g(\textbf{r})}{\partial \theta} \\ \\ \frac{1}{\tilde{r} \sin{\theta}}\frac{\partial g(\textbf{r})}{\partial \phi} \end{array}\right] \end{array} $$

(37)

and

$$ \begin{array}{@{}rcl@{}} &&\frac{1}{\tilde{r}^{2}} \frac{\partial}{\partial \tilde{r}} \left( \tilde{r}^{2} G(\tilde{r}) \frac{\partial g(\tilde{\textbf{r}})}{\partial \tilde{r}} \right) + \frac{H(\tilde{r})}{\tilde{r}^{2} \sin{\theta}} \left[ \frac{\partial}{\partial \theta} \left( \sin{\theta} \frac{\partial g(\tilde{\textbf{r}})}{\partial \theta} \right)\right.\\ &&\left.+ \frac{\partial^{2} g(\tilde{\textbf{r}})}{\partial \phi^{2}} \right] + \frac{1}{\tilde{r}^{2}} \frac{\partial}{\partial \tilde{r}} \left( \tilde{r}^{2} G(\tilde{r}) \frac{\partial \tilde{U}}{\partial \tilde{r}} \right) g(\tilde{\textbf{r}}) + G(\tilde{r}) \frac{d \tilde{U}}{d \tilde{r}} \frac{\partial g(\tilde{\textbf{r}})}{\partial \tilde{r}} \end{array} $$

(38)

If we neglect the lubrication forces acting on tangential directions we end up with

$$ \begin{array}{@{}rcl@{}} \frac{1}{\tilde{r}^{2}} \frac{\partial}{\partial \tilde{r}} \left( \tilde{r}^{2} G(\tilde{r}) \frac{\partial g(\tilde{\textbf{r}})}{\partial \tilde{r}} \right) + \frac{1}{\tilde{r}^{2}} \frac{\partial}{\partial \tilde{r}} \left( \tilde{r}^{2} G(\tilde{r}) \frac{d \tilde{U}}{d \tilde{r}} \right) g(\tilde{\textbf{r}})\\ +G(\tilde{r}) \frac{d \tilde{U}}{d \tilde{r}} \frac{\partial g(\tilde{\textbf{r}})}{\partial \tilde{r}}. \end{array} $$

(39)

Since every contribution from the angular coordinates disappeared it is possible to apply the angular average directly on the pcf on this portion of Eq. 17.

Appendix B: Angular averaging

In this section we describe the procedure where we describe the angular averaging procedure with which we evaluate $\langle \tilde {\textbf {v}} \rangle$ and $\langle \tilde {\nabla } \cdot \tilde {\textbf {v}} \rangle$. We start the procedure from Eq. 40

$$ \left\{\begin{array}{lll} \tilde{v}_{r} = \tilde{r} (1-A(\tilde{r}))\sin^{2}{\theta} \sin\phi \cos\phi \\ \tilde{v}_{\theta} = \tilde{r} (1- B(\tilde{r})) \sin{\theta} \cos{\theta}\sin\phi \cos\phi,\\ \tilde{v}_{\phi} = \tilde{r} \sin\theta\left( \cos^{2}\phi - \frac{B(\tilde{r})}{2} \cos(2 \phi) \right) \end{array}\right. $$

(40)

where $A(\tilde {r})$ and $B(\tilde {r})$ are functions representing the effect of the hydrodynamic disturbance along the radial and angular coordinate, respectively. Their values can be taken from the literature [8] and, in order to use them in the present analytical calculations, they are fitted through the following algebraic expressions [35]:

$$ \left\{\begin{array}{lll} A(\tilde{r}) = \frac{113.2568894}{(2 \tilde{r})^{5}} +\frac{307.8264828}{(2 \tilde{r})^{6}} +\\ - \frac{2607.54064288}{(2 \tilde{r})^{7}} + \frac{3333.72020041}{(2 \tilde{r})^{8}} \\\\ B(\tilde{r}) = \frac{0.96337157}{(2 \tilde{r} - 1.90461683)^{1.99517070}} +\\ - \frac{0.93850774}{(2 \tilde{r} - 1.90378420)^{2.01254004}}. \end{array}\right. $$

(41)

Our goal is to evaluate the average radial velocity in the area where the particles are approaching each other, which means the ensemble of angular coordinates $\tilde {v}_{r} < 0$.

It is found that the above mentioned condition is satisfied, for $\tilde {r} >0$, ∀𝜃 ∈ [0,π], ϕ ∈ [π/2,π] and ϕ ∈ [3π/2, 2π]. Now we apply the angular average obtaining:

$$ \begin{array}{@{}rcl@{}} \langle \tilde{\textbf{v}} \rangle_{\text{c}} &=& \tilde{r} (1-A(\tilde{r})) \frac{1}{4 \pi} \left[{\int}_{0}^{\pi} \sin^{2}(\theta) \sin\theta d\theta\right.\\ &&\left. \times \left( {\int}_{\pi/2}^{\pi} \sin(\phi) \cos(\phi) d \phi + {\int}_{3\pi/2}^{2 \pi} \sin(\phi) \cos(\phi) d \phi \right) \right]. \end{array} $$

(42)

Through this procedure we can obtain

$$ \alpha_{\text{c}} = -\frac{1}{3 \pi}. $$

(43)

To find the upstream region we need to impose $\tilde {v}_{r}>0$, which is given by ∀𝜃 ∈ [0,π], ϕ ∈ [0,π/2] and ϕ ∈ [π, 3π/2]. Applying the same procedure seen before for α_c we obtain:

$$ \begin{array}{@{}rcl@{}} \langle \tilde{\textbf{v}} \rangle_{\text{e}} &=& \tilde{r} (1-A(\tilde{r})) \frac{1}{4 \pi} \left[{\int}_{0}^{\pi} \sin^{2}(\theta) \sin\theta d\theta \times\right.\\ &&\left.\times \left( {\int}_{0}^{\pi/2} \sin(\phi) \cos(\phi) d \phi + {\int}_{\pi}^{3\pi/2} \sin(\phi) \cos(\phi) d \phi \right) \right], \end{array} $$

(44)

and, as a consequence

$$ \alpha_{\text{e}} = \frac{1}{3 \pi}. $$

(45)

From this point onward we will consider the compressional case only; the extensional one can be derived in a straightforward manner by replacing α_c with α_e.

Next we consider the divergence of the flow field, which can be written in spherical coordinates as

$$ \begin{array}{@{}rcl@{}} &&\tilde{\nabla} \cdot \tilde{\textbf{v}}\\ &=&\frac{1}{\tilde{r}^{2}} \frac{\partial}{\partial \tilde{r}} \left( \tilde{r}^{2} \tilde{v}_{r} \right) + \frac{1}{\tilde{r} \sin({\theta})} \frac{\partial}{\partial \theta} \left( \sin{\theta} v_{\theta} \right) + \frac{1}{\tilde{r} \sin{\theta}} \frac{\partial}{\partial \phi}\left( v_{\phi} \right). \end{array} $$

(46)

Adopting the correlations in Eq. 40, we can evaluate the divergence as

$$ \tilde{\nabla} \cdot \tilde{\textbf{v}} = \left[ 3 (B(\tilde{r})-A(\tilde{r}))-\tilde{r} \frac{\text{d}A}{\text{d}\tilde{r}} \right] \sin^{2}{\theta} \sin{\phi} \cos{\phi}. $$

(47)

Finally, we apply the integral average previously seen for 〈v〉_i and we obtain:

$$ \langle \tilde{\nabla} \cdot \tilde{\textbf{v}} \rangle_{\text{i}} = \alpha_{i} \left[ 3 (B(\tilde{r})-A(\tilde{r}))-\tilde{r} \frac{\text{d}A}{\text{d}\tilde{r}} \right], $$

(48)

with i = c,e for compression (c) and extension (e), respectively.