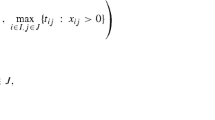Abstract
The relative error between best and worst solution of quadratic bottleneck assignment problems with cost coefficientsd ijpq =a ip b jq is considered, wherea ip is either arbitrarily given or corresponds to a distance in the plane. It is shown that the relative error is bounded by a function∈(m), tending to zero, with probability tending to one asm → ∞, provided the data are uniformly distributed. This implies that any algorithm for the above mentioned problems yields asymptotically an arbitrarily small relative error with probability tending to one.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R.E. Burkard, “Quadratische Bottleneck Probleme”,Operations Research Verfahren 18 (1974) 26–41.
R.E. Burkard and U. Fincke, “Probabilistic asymptotic properties of quadratic assignment problems”, Technical Report 81-3, Mathematisches Institut, Universität zu Köln, Cologne (February 1981).
R.M. Karp, “A patching algorithm for the nonsymmetric traveling-salesman problem”,SIAM Journal on Computing 8 (1979) 561–573.
S. Sahni and T. Gonzales, “P-complete approximation problems”,Journal of the Association for Computing Machinery 23 (1976) 555–565.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Burkard, R.E., Fincke, U. On random quadratic bottleneck assignment problems. Mathematical Programming 23, 227–232 (1982). https://doi.org/10.1007/BF01583791
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01583791